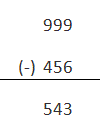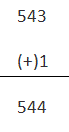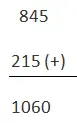在知道之前9的补充和10的补充我们应该知道为什么他们被使用以及为什么他们的概念存在。这些补充用于使数字系统中的算术运算更容易。在本文中,我们将讨论以下主题
- 9的补充
- 10的补充
- 9的补充减法
- 10的补充减法
现在,首先让我们知道9的补充是什么以及它是如何完成的。获得9的任何数字的补充,我们必须与数字减去(10N.- 1)其中n =数字中的数字数,或者以更简单的方式除以给定十进制数的每个数字用9.下面给出的表将更容易地解释9的补码。
| 十进制数字 | 9S补充 |
| 0. | 9. |
| 1 | 8. |
| 2 | 7. |
| 3. | 6. |
| 4. | 5. |
| 5. | 4. |
| 6. | 3. |
| 7. | 2 |
| 8. | 1 |
| 9. | 0. |
现在来临10的补充,在找出该号码的补充后,在找到10的补充后,相对容易。我们必须用1个9的补充任何数字都可以获得所需的10个数字的补充。或者如果我们想直接找出10年代的补充,我们可以通过以下公式进行,(10N.- 数字),其中n =数字中的数字数。下面给出一个例子来说明获得10个补充的概念。
让我们占用十进制数字456,9的补码将是
10的补充没有
9的补充减法
我们将通过示例理解这种减法方法
A = 215.
B = 155.
我们想通过9的补充减法方法找到A-B
首先,我们必须找出9的补充B
现在我们必须添加9的补充b到a
结果的最左键称为携带,并将其添加回到结果的部分
给出了另一种不同类型的示例
a = 4567.
B = 1234.
我们需要找出a - b
9的b补充b
8765
加入9的B补充B
使用我们得到的结果加入携带
3333
现在答案是 - 3333
NB:如果没有携带答案将是 - (9的答案补充)
减法10的补充
我们将通过一个例子来显示该过程
采取相同的数据
A = 215.
B = 155.
10的B = 845的补充
增加了10的B到a
在这种情况下,省略携带
答案是60
采取其他例子
a = 4567.
B = 1234.
10的B = 8766的补充
添加10的B与a的补充
为了得到答案,仍然被忽略
所以,答案是 - 3333
注意:如果有携带然后答案是 - (10年代获得的总和)