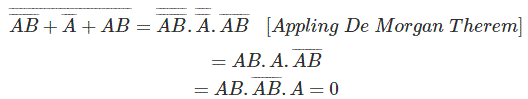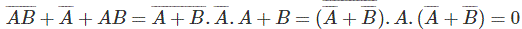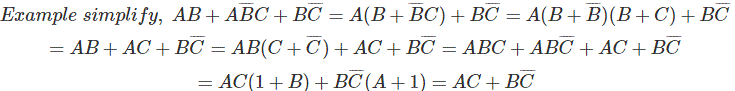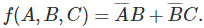布尔代数定理与布尔代数定律

什么是布尔代数？

布尔代数是一种不同的代数，而是可以说是一个新的代数，由世界着名的数学家乔治·斗篷在1854年中发明。他在他的书中发表了“思想法律的调查”。

后来使用这种技术克劳德香农推出了一种被称为的新型代数切换代数。在数字电子产品，有几种方法可以简化逻辑电路的设计。这个代数就是其中一种方法。

根据George Bole符号可以用来代表逻辑思想的结构。这种代数涉及被称为的规则或法律布尔代数法律通过该逻辑操作进行。

也有少数布尔代数定理，需要仔细注意到，因为这些使得计算最快，更容易。Boolean逻辑处理只有两个变量，1和0，由此进行所有数学操作。

布尔代数或切换代数是一个数学逻辑系统，用于在a中执行不同的数学运算二元系统。只有三个基础操作，或者，而不是所有简单的和复杂的二进制数学运算都是要完成的。

在布尔代数中有许多规则，这些规则是用来进行数学运算的。在布尔代数中，变量用英文大写字母表示，如A, B, C等，每个变量的值可以是1或0，没有其他的。

在布尔代数中，给出的表达式也可以转换为使用不同的逻辑图逻辑门喜欢和门那或门和非门那也不是盖茨那NAND盖茨那XOR门那Xnor盖茨， 等等。

一些基本的逻辑布尔操作，
和操作
或操作
不经营

布尔代数的一些基本法律

一种 。0 = 0，其中A可以为0或1。
一种 。1 = A可以为0或1的位置。
一种 。a = a，其中a可以是0或1。
一种 。Â= 0其中A可以是0或1。
A + 0 = A A可以是0也可以是1。
A + 1 = 1 A可以是0也可以是1。
a +Â= 1
A + A = A
A + B = B + A，其中A和B可以是0或1。
一种 。b = b。A和B可以为0或1的位置。
布尔代数定律也适用于两个以上的变量，比如，

布尔代数累积法

根据累积法，订单或运营和和运营在变量上进行没有差异。

Boolean代数的联想法律

本法是用于多个变量，其中变量结果的或通过分组变量的相同。在案例和运营商的情况下，这项法律是相同的。

布尔代数的分配法

本法由两名运营商组成，或者。

让我们显示这种法律的一个使用来证明表达

证明：

冗余文字规则

来自真相表那

输入			输出
一种	B.	AB	a +Âb.
0.	0.	0.	0.
0.	1	1	1
1	0.	0.	1
1	1	0.	1

输入		输出
一种	B.	A + B.
0.	0.	0.
0.	1	1
1	0.	1
1	1	1

从真相表中，证明，

布尔代数的吸收定律

真理表的证明，

输入			输出
一种	B.	ab	A + A.B.
0.	0.	0.	0.
0.	1	0.	0.
1	0.	0.	1
1	1	1	1

a和a + a.b列都是相同的。

证明真相表那

一种	B.	A + B.	A.X（A + B）
0.	0.	0.	0.
0.	1	1	0.
1	0.	1	1
1	1	1	1

A和A.X或A(A+B)列是相同的。

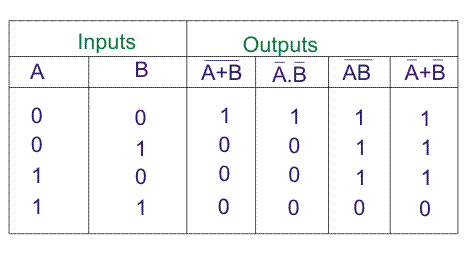
从de Morgan的定理那

真理表的证明，

布尔代数的例子

这是另一种简化复杂布尔表达式的方法。在这个方法中，我们只使用三个简单的步骤。

1. 补充整个布尔表达式。
2. 将所有或者更改为和所有和所有和所有。
3. 现在，补充每个变量并获得最终表达式。

通过这种方法,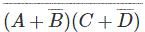
我将首先补充，即。现在，将所有（+）更改为（。）和（。）到（+）即（+）即。现在，对每个变量进行补充，这是Boolean表达式的最终简化形式，

它完全等于通过施用而来的结果de摩根定理。
另一个例子，

用第二种方法，


Boolean函数的表示真相表。
让我们考虑一个布尔函数，

现在让我们代表真相表中的函数。

因此，我们已经显示了一些基本布尔代数法律。在其他页面上，我们描述了De Morgan的定理和相关法律。