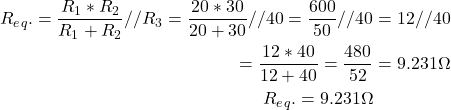当前分频器：它是什么？公式，规则和例子|英雄联盟菠菜app电气4U. - 英雄联盟菠菜app,英雄联盟赌钱网站,英雄联盟彩票官网首页

内容

什么是当前分频器？

分频器被定义为线性电路，该线性电路产生作为其输入电流的一小部分的输出电流。这是通过连接并联连接的两个或更多个电路元件来实现的当前的在每个分支中总是会以这样的方式划分，使总数能源在电路中消耗至少是最小的。

换句话说，在并联电路，电源电流分裂成多个并行路径。它也被称为“当前分配规则”或“当前分配法”。

并行电路通常被称为电流分频器，其中所有组件的终端以它们共享相同的两个端连接节点．这些会导致电流通过不同的平行路径和分支。

因此，电流在所有分支的并联电路是不同的电压在所有连接的路径上都是一样的。IE。 $V_r_1 = v_r_2 = v_r_3$ ．．．．等。因此，没有必要找到每一个之间的单个电压电阻器这使得分支电流很容易被发现基尔霍夫电流定律和欧姆定律。

而且，在并联电路中，等效电阻总是小于任何单独的电阻。

当前分频器公式

给出了分流器的通用公式

$\{对齐*}开始I_X = I_T[\压裂{R_T} {R_X}] \{对齐*}结束$

在那里,

$I_X$ 通过并联电路中任意电阻的电流 $\压裂{V} {R_X}$

$I_T$ =电路总电流= $\ frac {v} {r_t}$

$r_t.$ =等价物抵抗性平行电路

$V$ 平行电路上的电压= $I_T R_T$ ＝ $I_X R_X$ （随着电压的所有组件相同）

按照阻抗，当前分频器的公式给出

$\ begin {aligne *} i_x = i_t [\ frac {z_t} {z_x}] \ neg {align *}$

按照导纳，当前分频器的公式给出

${对齐*}\开始I_X = I_T[\压裂{Y_X} {Y_T }] \,\,\,\, ( \ \, Z = \压裂{1}{Y})结束\{对齐*}$

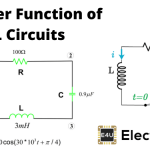
电流分频公式RC并联电路

对上述电路施加分流规则，通过电阻的电流为:

$\ begin {align *} i_r = i_t [\ frac {z_c} {r + z_c}] \ neg {align *}$

在那里, $Z_C.$ =阻抗电容器＝ $j \ \压裂{1}{ωC}$

因此我们得到了，

$\ begin {aligne *} \ begin {split *}＆i_r = i_t [\ frac {\ frac {1} {j \ oomga c}} {r + \ frac {1} {j \ oomga c}}] \\ =i_t [\ frac {\ frac {1} {j \ omega c}} {j \ oomga c}} {j \ omega c}}] \\ \ end {split *} \结束{align *}$

$\{对齐*}开始I_R = I_T[\压裂{1}{1 + jωRC} \] \{对齐*}结束$

当前分频规则推导

考虑一个由两个电阻R组成的并联电路₁和R₂通过V伏电压的电源连接。

假设进入电阻器的并联组合的总电流是i_T．总电流i_T分为两部分₁和我₂在哪里我₁流过电阻R的电流是多少₁和我₂流过电阻R的电流是多少_2.

因此，总电流为

（1） $\ begin {arearation *} i_t = i_1 + i_2 \ end {arequation *}$

或

（2） $\begin{equation*} I_1 = I_T-I_2 \end{equation*}$

或

（3） $\begin{equation*} I_2= I_T-I_1 \end{equation*}$

现在，当两个电阻并联连接时，等效电阻器r_情商是由

$\begin{align*} R_e_q = R_1 // R_2 \end{align*}$

（4） $\{方程*}R_e_q开始= \压裂{R_1 * R_2} {R_1 + R_2} \{方程*}结束$

根据欧姆定律。 $R I = \压裂{V} {}$ ，表示流过电阻R的电流₁是由

$\ begin {align *} i_1 = \ frac {v} {r_1} \ neg {align *}$

(5） $\ begin {arearation *} v = i_1 r_1 \ end {arequation *}$

类似地，电流流过电阻器r₂是由

$\begin{align*} I_2 = \frac{V}{R_2} \end{align*}$

（6） $\ begin {arearation *} v = i_2 r_2 \ end {arequation *}$

比较方程（5）和（6）我们得到，

$\begin{align*} V = I_1 R_1 = I_2 R_2 \end{align*}$

$\ begin {aligne *} i_1 = i_2 \ frac {r_2} {r_1} {r_1} \ end {align *}$

把这个值放在我的价值₁进入等式（1）我们得到，

${对齐*}\ \开始开始{分裂*}& I_T = I_2 \压裂{R_2} {R_1} + I_2 \ \ = I_2[\压裂{R_2} {R_1} + 1] \ \ = I_2[\压裂{R_2 + R_1} {R_1}] \{分裂*}结束\{对齐*}结束$

（7） $\ begin {arearation *} i_2 = i_t [\ frac {r_1} {r_1 + r_2}] \ neat {公式*}$

现在把I的方程代入₂对式(2)有

$\ begin {align *} \ begin {split *}＆i_1 = i_t - i_t [\ frac {r_1} {r_1 + r_2}] \\ = i_t [1- \ frac {r_1} {r_1 + r_2}] \\= i_t [\ frac {r_1 + r_2-r_1} {r_1 + r_2}] \ end {split *} \ end {align *}$

（8） $\ begin {arearation *} i_1 = i_t [\ frac {r_2} {r_1 + r_2}] \ neat {公式*}$

因此，由式(7)和式(8)我们可以说，任何支路的电流等于对支路电阻与总电阻值的比值，乘以电路中的总电流。

一般来说，

$\ \ \ \,分支,目前\ \,= \ \,总\ \,当前*(\压裂{阻力\,\ \ \,相反\ \,分支}{总和\,\ \ \,,\ \,阻力\ \,的\ \,,\ \,两个\ \,分支})$

当前分配器例子

具有电流源的2个电阻的电流分频器

例1：考虑两个电阻20Ω和40Ω，与电流源20 A平行连接。找出通过并联电路中的每个电阻流过的电流。

鉴于数据:R₁= 20Ω,R₂= 40Ω和我_T= 20 A.

电流通过电阻r₁是由

${对齐*}\ \开始开始{分裂}& I_1 = I_T[\压裂{R_2} {R_1 + R_2}] = 20[\压裂{40}{20 + 40}]= 20[\压裂{40}{60}]= 20[0.67]= 13.33 \{分裂}结束\结束{对齐*}$

（9） $\begin{equation*} I_1 = 13.33 A \end{equation*}$

电流通过电阻r₂是由

${对齐*}\ \开始开始{分裂}& I_2 = I_T[\压裂{R_1} {R_1 + R_2}] = 20[\压裂{20}{20 + 40}]= 20[\压裂{20}{60}]= 20[0.33]= 6.67 \{分裂}结束\结束{对齐*}$

(10） $\ begin {arearation *} i_2 = 6.67 A \ END {equation *}$

现在，添加等式（9）和（10）我们得到，

$\begin{align*} I_1 + I_2 = 13.33 + 6.67 = 20 A = I_T \end{align*}$

根据基尔霍夫电流法则，所有支路电流等于总电流。因此，我们可以看到总电流(I_T)是根据支路电阻所确定的比率来划分的。

具有2个电阻的电流分频器与电压源并联

例2.:考虑两个电阻10Ω和20Ω与a并联电压源50 V。求出总电流的大小和流过并联电路中每个电阻的电流。

鉴于数据:R₁= 10Ω,R₂=20Ω和v = 50 v

并联电路的等效电阻为:

$\ begin {align *} \ begin {split}＆r_e_q。= \ FRAC {R_1 * R_2} {R_1 + R_2} = \ FRAC {10 * 20} {10 + 20} = 6.67 \ OMEGA \ END {SPLIT} \ END {alight *}$

根据欧姆定律，流过并联电路的总电流为:

$\ begin {align *} \ begin {split}＆i_t = \ frac {v} {r_e_q。} = \ frac {50} {6.67} = 7.5 a \ neat {split} \ end {alight *}$

现在，根据当前分频器公式的电流通过电阻器r₁是由

${对齐*}\ \开始开始{分裂}& I_1 = I_T[\压裂{R_2} {R_1 + R_2}] = 7.5[\压裂{20}{10 + 20}]= 7.5[\压裂{20}{30})= 7.5(0.67)= 5 \{分裂}\{对齐*}结束结束$

（11） $\begin{等式*}I_1 = 5 A \end{等式*}$

电流通过电阻r₂是由

${对齐*}\ \开始开始{分裂}& I_2 = I_T[\压裂{R_1} {R_1 + R_2}] = 7.5[\压裂{10}{10 + 20}]= 7.5[\压裂{10}{30})= 7.5(0.33)= 2.5 \{分裂}结束\结束{对齐*}$

（12） $\begin{equation*} I_2 = 2.5 A \end{equation*}$

现在，加上方程(11)(12)我们得到，

$\ begin {align *} i_1 + i_2 = 5 + 2.5 = 7.5 a = i_t \ neg {align *}$

根据基尔霍夫电流法则，所有支路电流等于总电流。因此，我们可以看到总电流(I_T)是根据支路电阻所确定的比率来划分的。

并联3个电阻的分流器

例3.:考虑三个电阻20Ω， 30Ω和40Ω并联形成如下图所示的分流电路。电路与100V电源相连。用电流分划法求出并联电路的总电流和流过各电阻的电流。

鉴于数据:R₁= 20Ω,R₂=30Ω，r_3.=40Ω和v = 100 v

并联电路的等效电阻为:

$\ begin {align *} \ begin {split} r_e_q。= \ frac {r_1 * r_2} {r_1 + r_2} // r_3 = \ frac {20 * 30} {20 + 30} // 40 = \ frac {600} {50} // 40＆= 12 // 40\\ = \ FRAC {12 * 40} {12 + 40} = \ FRAC {480} {52}＆= 9.231 \ oomega \\ r_e_q。= 9.231 \ omega \ end {split} \ end {alight *}$

根据欧姆定律，流过并联电路的总电流为:

${对齐*}\ \开始开始{分裂}& I_T = \压裂{V} {R_e_q。} = \frac{100}{9.231} = 10.83 A \end{split} \end{align*}$

现在，根据分流公式，通过电阻R的电流₁是由

${对齐*}\ \开始开始{分裂}& I_1 = I_T[\压裂{R_e_q。} {R_1}] = 10.83[\压裂{9.231}{20}]= 10.83(0.46)= 4.999 \{分裂}结束\结束{对齐*}$

（13） $\begin{equation*} I_1 = 4.999 A \end{equation*}$

电流通过电阻r₂是由

$\ begin {align *} \ begin {split}＆i_2 = i_t [\ frac {r_e_q。} {r_2}] = 10.83 [\ frac {9.231} {30}] = 10.83 [0.31] = 3.33 A \ END {split} \结束{align *}$

（14） $\ begin {arequation *} i_1 = 3.33 A \ END {equation *}$

类似地，通过电阻R的电流_3.是由

${对齐*}\ \开始开始{分裂}& I_3 = I_T[\压裂{R_e_q。} {R_3}] = 10.83[\压裂{9.231}{40}]= 10.83(0.12)= 2.499 \{分裂}结束\结束{对齐*}$

（15） $\ begin {arearation *} i_1 = 2.499 A \ END {公式*}$

现在，添加等式（13），（14）和（15）我们得到，

$\ begin {align *} i_1 + i_2 + i_3 = 4.999 + 3.33 + 2.499 = 10.83 a = i_t \ neg {align *}$

根据基尔霍夫电流法则，所有支路电流等于总电流。因此，我们可以看到总电流(I_T)是根据支路电阻所确定的比率来划分的。

请注意，从所有的三个例子中，我们可以说，电阻越小，电流所占的份额越大，反之亦然。同时，电源电流等于各支路电流之和。

当您可以使用当前分频器规则时

您可以在以下情况下使用当前的分频规则:

当两个或多个电路元件与电压源或电流源并联时，使用电流分流规则。

当已知电路的总电流和等效电阻时，电流分配器规则也可以用来确定各个支路的电流。

当两个电阻连接在平行电路中时，任何分支中的电流将是总电流的一小部分（I_T)）.如果两个电阻器是相等的值，那么电流将相等地通过两个支路。

当三个或更多的电阻并联时，等效电阻(R_eq。)用于将总电流分成并联电路中各支路的小电流(见例3)。