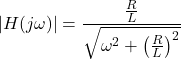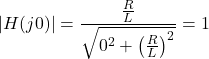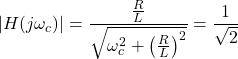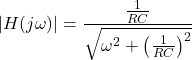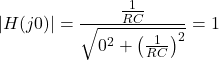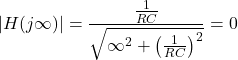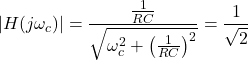截止频率:什么?方程&如何找到它英雄联盟菠菜app - 英雄联盟菠菜app,英雄联盟赌钱网站,英雄联盟彩票官网首页

内容

什么是截止频率?

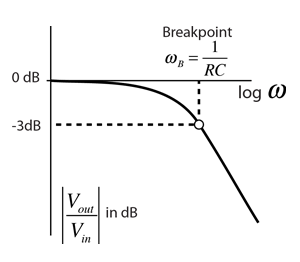
截止频率(也称为拐角频率，或中断频率)定义为系统频率响应中的一个边界，在这个边界处，流经系统的能量开始衰减(反射或减少)，而不是通过。

在电子学中，截止频率或角频率是电路(如线路)的输出功率高于或低于该频率的频率。放大器，或电子过滤器(例如高通滤波器)已降至通频带中给定的功率比例。

最常见的情况是，这个比例是通频带功率的一半，也称为3db点，因为3db的下降大约相当于一半功率。作为电压比，这是一个下降到大约0.707。

适用于任何滤波电路，如RC电路，截止频率是一个非常重要的特性。此时，由于滤波器的衰减量开始迅速增加。

表示多长时间放大器增益可以保持频率不变，我们需要定义一个频率范围。在此范围内，增益的偏差不应超过中频基准最大增益的70.7%。在下面的曲线中，f1和f2分别表示下截止频率和上截止频率。

带宽

在信号处理中，带宽被定义为上截止频率和低截止频率之间的差异。频率F2沿着低频范围内的高频范围和F1位于频率范围内。我们还可以将这两个频率命名为半功率频率电压增益降至最大值的70.7%。

这表示中频参考频率功率的一半的功率水平。由于变化是不明显的，音频放大器有一个平坦的响应从f1到f2。

截止频率方程

截止频率(转角频率)公式为

$开始\ f c{} ={对齐*}\压裂{1}{2 \πRC} \{对齐*}结束$

其中R和C是电阻和电容．一个简单的RC低通滤波器，截止（3DB点）被定义为当电阻与电容电抗的幅度相同时

分贝单位

增益通常用分贝表示。分贝单位是人耳对声音强度的对数响应。因此分贝是一个功率与另一个功率之比的对数测量值，它也可以表示为一个电压与另一个电压之比。

一般情况下，放大器的电压输出或电压增益用分贝(dB)表示，分贝为电压增益(dB) $20日志Av$ ．

放大器的功率增益用分贝(dB)表示，分贝由功率增益(dB)给出 $10日志美联社$

当一个_v大于1，则dB增益为正。它代表着放大。当一个_v小于1,dB是负的。它代表衰减。

在放大器中，在少数情况下，增益值可以分配为0 dB参考值。在这种情况下，它意味着参考增益被用作比较其他增益值的参考增益。

放大器在中频范围内显示最大增益，在低频范围内显示较小增益。最大增益称为值为0 dB的中频范围。当增益值低于中频范围时，表示为负的dB值。

如何找到截止频率

计算截止频率的方法有很多种。

传递函数的截止频率

对正弦源频率变化的电路的分析称为电路的频率响应。的传递函数定义为s域中输出电压与输入电压之比。

$\{方程*}开始H (s) = \压裂{V_ {0} (s)} {V_{我}(s)} \{方程*}结束$

当使用正弦电源时，传递函数将被给出为输出电压的幅值和相位到电路中输入电压的幅值和相位。在这种情况下， $j \ω$ Will被用来代替s。

$\{对齐*}开始H (s) = \压裂{V_ {0} (j \ω)}{V_{我}(j \ω)}\{对齐*}结束$

例如，考虑传递函数

$\{对齐*}开始H (s) = \压裂{20 (s + 10)} {s + 100)} \{对齐*}结束$

由上式求得角点频率，H(s)可代入为

（1） $\{对齐*}开始H (s) = \压裂{2 (1 + s / 10))} {1 + (s / 100))} \{对齐*}结束$

（2） $开始\{对齐*}2 (1 + (s / 10)) \压裂{1}{(1 + (s / 100))} \枚H_ {1} (s) H_{2}结束(s) \{对齐*}$

因此，由这个方程，角点频率计算为 $\ omega_ {01} (s) = 10 rad / s$ 和 $\ omega_ {02} (s) = 100 rad / s$ ．为了选择频率范围，必须考虑角频的取值。

波德图的截止频率

一种常用的图表控制系统工程测定a的稳定性控制系统被称为一个波德图．波德图用两幅图概括了系统的频率响应——波德幅度图(以分贝表示幅度)和波德相位图(以度数表示相移)。

在波德图中，角频率定义为两条渐近线相交或相交的频率。

传递函数 $H (s) = \压裂{V_ {0} (s)} {V_{我}(s)}$ 一个系统的增益和稳定性承载了大量的信息。波德图给出给定物体的估计图像
$H(年代)$ 从中可以得到系统增益及其稳定性的一个合理的概念
实现。

低通滤波器的截止频率

低通滤波器是一种允许低频信号而阻止高频信号的电路。所有低通滤波器都有一定的截止频率，超过该截止频率，输出电压降至输入电压的70.7%以下。幅度响应比0hz的值低3db的频率，称为低通滤波器的截止频率。

例如，如果低通电容滤波器具有 $R = 500 \ω$ 和 $C = 7 \μF$ ，在什么频率下输出为70.7%?

带有一个电阻和一个电容的简单电容低通滤波器的截止频率为 $f c{} = \压裂{1}{2 \πRC}$ ．代入相应的R和C值，则截止频率为45.473 Hz。因此，在45.473 Hz时输出将为70.7%。

当波德图被绘制为低通滤波器如下图所示，低频滤波器的频率响应似乎是几乎平坦的。

直到截止频率点，所有的输入信号直接传递到输出，这导致一个单位增益。当电容器的电抗在低频率时就会发生这种情况，防止任何电流通过电容器。电路的响应在这个截止频率点之后以-20dB/ Decade“滚转”的斜率降至零。

容抗和电阻相等的频率点称为低通滤波器的截止频率。在截止频率处，输出信号衰减到输入信号值的70.7%或3 db的输入。

考虑一个带有传递函数的一阶低pas滤波器

$开始\{对齐*}T (s) = \压裂{现代{0}}{s + \ω_{0}}{对齐*}\结束$

用RC除分子和分母来改写上面的方程

（3) $开始\{对齐*}T (s) = \压裂{1}{1 + sRC} \{对齐*}结束$

（4) $开始\{对齐*}T (s) = \压裂{1 / RC} {s + 1 / RC} \{对齐*}结束$

因此, $A_ {0} = 1 / RC$ 和 $\ omega_ {0} = 1 / RC$ ,在那里 $\ omega_ {0}$ 为截止频率。

为了更好地理解截止频率，将标准的s域传递函数转换为等价的 $j \ω$ 格式。

$开始\{对齐*}T (s) = \压裂{K} {1 + s /ω\ _{0}}{对齐*}\结束$

$开始\{对齐*}T (j \ω)= \压裂{K} {1 + \ j{\压裂{\ω}{\ omega_{0}}}}{对齐*}\结束$

现在，让我们在截止频率处计算这个表达式

$开始\{对齐*}T (jω= \ \ omega_{0}) = \压裂{K} {1 + \ j{\压裂{\ω}{\ omega_{0}}}} = \压裂{K} {1 + j} \{对齐*}结束$

如果分母是复数，则需要计算模的大小。

${对齐*}\ \开始左| T (jω= \ \ omega_{0}) \右| = \压裂{K}{\√6{1 ^{2}}+ 1 ^{2}}= \压裂{K} {\ sqrt{2}}{对齐*}\结束$

K是直流增益。当输入频率增加到截止频率时，输出振幅为 $\压裂{K} {\ sqrt {2}}$ ．的值 $\压裂{1}{\ sqrt {2}}$ 对应的是-3dB，也就是截止频率。

该传递函数分析表明，截止频率仅仅是滤波器的幅度响应的频率，其对应于极低频率幅度响应的3dB。

高通滤波器的截止频率

一个高通滤波器通过频率大于指定截止频率的信号。它对频率低于截止频率的信号进行衰减。

传递函数由下式导出。

$R \{对齐*}开始Z_ {} = R \;\;和\;\;Z_ {C} = \压裂{1}{sC} \{对齐*}结束$

输出阻抗为

$\{对齐*}开始Z_{出}= Z_ {R} \{对齐*}结束$

输入阻抗为

$\{对齐*}开始Z_ {} = Z_ {R} + Z_ C{} \{对齐*}结束$

高通滤波器的传递函数定义为输出电压与输入电压的比值。

$\ begin {align *} \ frac {v_ {out}} {v_ {in}} = \ frac {z_ {out}} {z_ {in}} \ neg {align *}$

${对齐*}= \ \开始压裂{Z_ {R}} {Z_ {R} + Z_ {C}}{对齐*}\结束$

${对齐*}= \ \开始压裂{R} {R + \压裂{1}{sC}}{对齐*}\结束$

${对齐*}= \ \开始压裂{可控硅}{可控硅+ 1}T (S) \{对齐*}结束$

${对齐*}= \ \开始压裂{年代}{s + \压裂{1}{RC}}{对齐*}\结束$

将上述方程与传递函数的标准形式进行比较，

$\ begin {aligne *} t（s）= \ frac {a_ {a_1} s} {s + \ oomega _ {0}} \ neg {align *}$

$现代{1}$ 是信号的振幅吗

$ω\ _ {0}$ 角截止频率是多少

截止频率是指在通带和阻带之间产生边界的频率。如果信号频率大于高通滤波器的截止频率，那么它将导致信号通过。一阶高通滤波器的截止频率方程与低通滤波器相同。

$开始\ f c{} ={对齐*}\压裂{1}{2 \πRC} \{对齐*}结束$

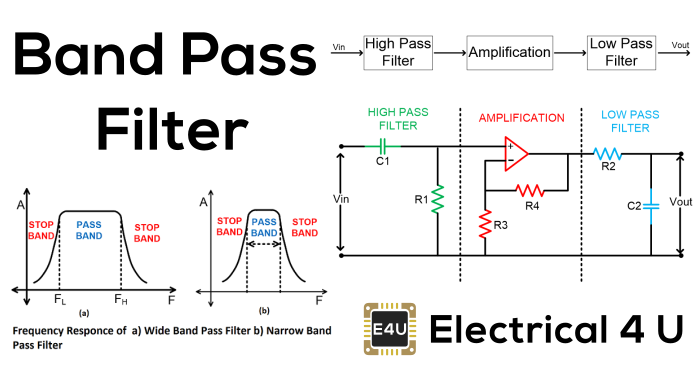
带通滤波器的截止频率

的带通滤波器由两个截止频率组成。带通滤波器由高通滤波器和低通滤波器组成。第一个截止频率来自高通滤波器，称为较高截止频率。这个截止频率被称为fc高。

$\{对齐*}开始FC_{高}= \压裂{1}{2 \πR_ {1} C_{1}}{对齐*}\结束$

第二个截止频率来自于低通滤波器，称为较低截止频率。这个截止频率被称为fc低。

$\{对齐*}开始FC_{低}= \压裂{1}{2 \πR_ {2} C_{2}}{对齐*}\结束$

带宽是这些频率之间的范围。对于高通滤波器，截止频率将定义带宽的较低值。对于低通滤波器，截止频率将定义较高的带宽值。

RL电路的截止频率

考虑一个简单的RL电路如下所示。

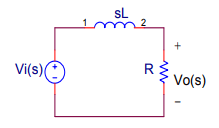
其传递函数为

${对齐*}\ \开始压裂{V_ {0} (s)} {V_{我}(s)} = \压裂{R} {sL + R} \{对齐*}结束$

$\{对齐*}开始H (s) = \压裂{\压裂{R} {L}} {s + \压裂{R} {L}}{对齐*}\结束$

替代 $s = j \ω$ 在上面的等式中计算频率响应

$H (j \ \{对齐*}开始ω)= \压裂{\压裂{R} {L}} {j \ω+ \压裂{R} {L}}{对齐*}\结束$

级响应

${对齐*}\ \开始左右| H (j \ω)\ | = \压裂{\压裂{R} {L}}{\√6{\ω^{2}+ \离开(\压裂{R}{1} \右)^{2}}}{对齐*}\结束$

当 $\ω$ = 0

${对齐*}\ \开始左右| H (j₀)\ | = \压裂{\压裂{R} {L}}{\√6{0 ^{2}+ \离开(\压裂{R}{1} \右)^{2}}}= 1 \{对齐*}结束$

当 $\ω$ ＝ $\ infty$

${对齐*}\ \开始左右| H (j \ infty) \ | = \压裂{\压裂{R} {L}}{\√6 {\ infty ^{2} + \离开(\压裂{R}{1} \右)^{2}}}= 0 \{对齐*}结束$

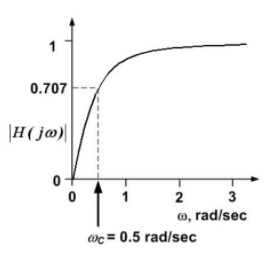
为了计算截止频率，

${对齐*}\ \开始左右| H (j \ omega_c) \ | = \压裂{\压裂{R} {L}}{\√6 {\ omega_c ^{2} + \离开(\压裂{R}{1} \右)^{2}}}= \压裂{{1}}{\ sqrt{2}}{对齐*}\结束$

最后，给出了RL电路的截止频率

${对齐*}\ \开始omega_ {c} = \压裂{R}{1} \{对齐*}结束$

RC电路的截止频率

考虑一个简单的RC电路如下所示。

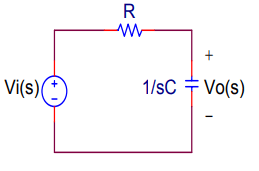
其传递函数为

${对齐*}\ \开始压裂{V_ {0} (s)} {V_{我}(s)} = \压裂{\压裂{1}{sC}} {R + \压裂{1}{sC}}{对齐*}\结束$

$\{对齐*}开始H (s) = \压裂{\压裂{1}{RC}} {s + \压裂{1}{RC}}{对齐*}\结束$

替代 $s = j \ω$ 在上面的等式中计算频率响应

$H (j \ \{对齐*}开始ω)= \压裂{\压裂{1}{RC}} {j \ω+ \压裂{1}{RC}}{对齐*}\结束$

级响应

${对齐*}\ \开始左右| H (j \ω)\ | = \压裂{\压裂{1}{RC}}{\√6{\ω^{2}+ \离开(\压裂{1}{RC} \右)^{2}}}{对齐*}\结束$

当 $\ω$ = 0

${对齐*}\ \开始左右| H (j₀)\ | = \压裂{\压裂{1}{RC}}{\√6{0 ^{2}+ \离开(\压裂{1}{RC} \右)^{2}}}= 1 \{对齐*}结束$

当 $\ω$ ＝ $\ infty$

${对齐*}\ \开始左右| H (j \ infty) \ | = \压裂{\压裂{1}{RC}}{\√6 {\ infty ^{2} + \离开(\压裂{1}{RC} \右)^{2}}}= 0 \{对齐*}结束$

为了计算截止频率，

${对齐*}\ \开始左右| H (j \ omega_c) \ | = \压裂{\压裂{1}{RC}}{\√6 {\ omega_c ^{2} + \离开(\压裂{1}{RC} \右)^{2}}}= \压裂{{1}}{\ sqrt{2}}{对齐*}\结束$

最后，给出了RL电路的截止频率

${对齐*}\ \开始omega_ {c} = \压裂{1}{RC} \{对齐*}结束$