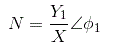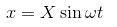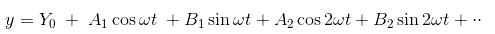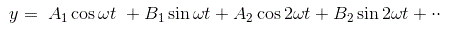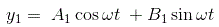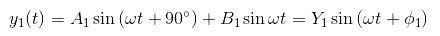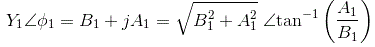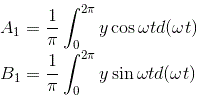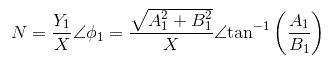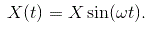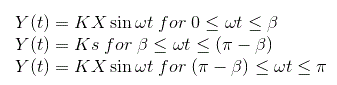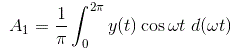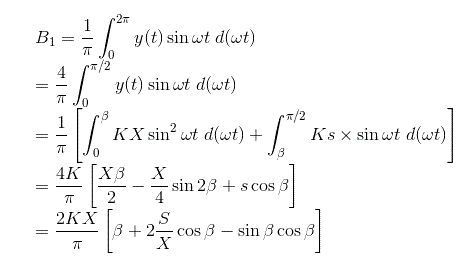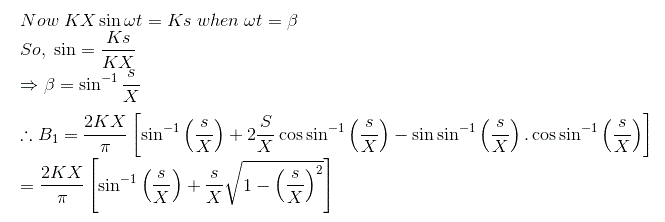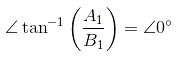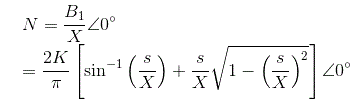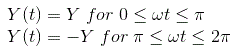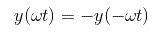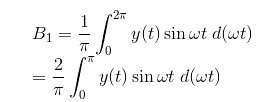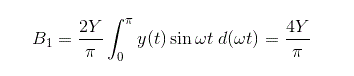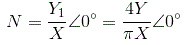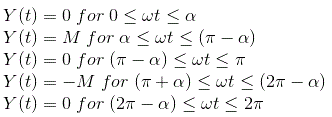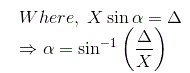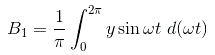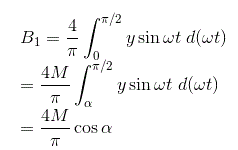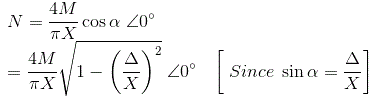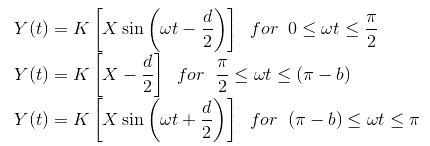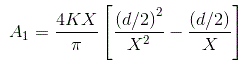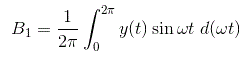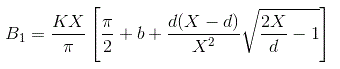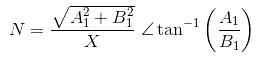的描述函数分析某些非线性控制问题的近似方法是什么控制工程.首先,让我们回顾一下线性控制系统的基本定义。线性控制系统是那些叠加原则(如果同时应用两个输入,则输出将是两个输出的总和)。在高度非线性控制系统的情况下,我们无法应用叠加的原理。
由于不同的非线性控制系统的非线性特性,对其进行分析是非常困难的。我们不能使用传统的分析方法,如奈奎斯特稳定性判据或辐射方法以分析这些非线性系统,因为这些方法仅限于线性系统。也就是说,非线性系统有一些优点:
- 非线性系统比线性系统性能更好。
- 非线性系统比线性系统成本低。
- 与线性系统相比,它们通常体积小而紧凑。
在实践中,所有的物理系统都有某种形式的非线性。有时,为了提高系统的性能或使其运行更安全,甚至有意引入非线性是可取的。结果表明,该系统比线性系统更经济。
具有有意引入的非线性的系统的最简单示例之一是继电器控制或开/关系统。例如,在典型的家用加热系统中,当温度低于某个指定值时,炉子导通,当温度超过另一个给定值时,当温度低于某个指定值。在这里,我们将讨论两种不同类型的分析或用于分析非线性系统的方法。下面写的两种方法并在示例的帮助下简要讨论。
- 描述函数控制系统方法
- 控制系统中的相平面方法
常见的非线性
在大多数控制系统类型,我们无法避免某些类型的存在非线性.这些可以分为静态和动态。输入和输出之间存在非线性关系而不涉及微分方程的系统称为静态非线性系统。另一方面,输入和输出可以通过非线性微分方程联系起来。这样的系统称为动态非线性系统。
现在我们将讨论各种类型的控制系统中的非线性:
- 饱和非线性
- 摩擦非线性
- 死区非线性
- 继电器非线性(在控制器上)
- 强烈的非线性
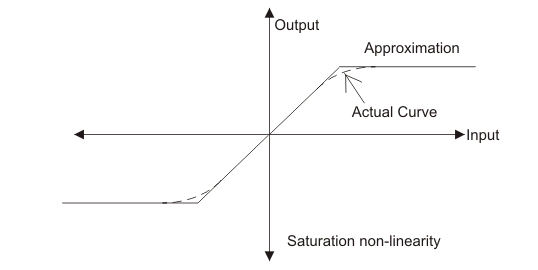
饱和非线性
饱和非线性是一种常见的非线性类型。例如,在磁化曲线中看到这种非线性直流电机.为了理解这种类型的非线性,让我们讨论下面给出的饱和曲线或磁化曲线:
从上面的曲线来看,我们可以看到输出在开始时显示线性行为,但之后存在在系统中一种非线性的曲线中的饱和度。我们也显示了近似的曲线。
相同类型的饱和非线性我们还可以看到,在放大器中,只有在有限的输入值范围内,输出与输入成比例。当输入超过这个范围时,输出趋于非线性。
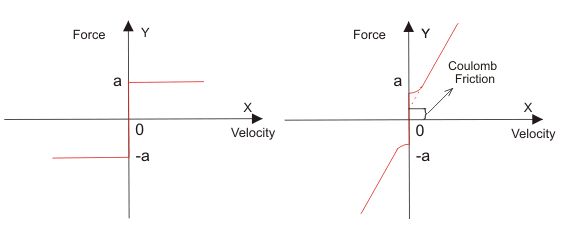
摩擦非线性
任何与物体的相对运动相抵触的东西叫做摩擦力。它是系统中存在的一种非线性。an中常见的例子电竞外围投注app靠谱么其中,由于电刷和换向器之间的摩擦接触,我们发现库仑摩擦阻力。
摩擦可能有三种类型,如下所述:
- 静态摩擦:简单地说,当物体静止时,静摩擦作用于物体。
- 动态摩擦:当物体与表面作相对运动时,动摩擦作用于物体上。
- 限制摩擦:它被定义为限制摩擦的最大值,该摩擦在休息时作用于身体。
动摩擦也可分为(a)滑动摩擦(b)滚动摩擦。滑动摩擦作用于两个物体在对方身上滑动,而滚动作用于物体在另一个物体上滚动。
在机械系统中,我们有两种类型的摩擦即(a)粘性摩擦(b)静态摩擦。
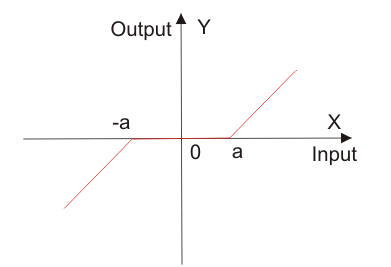
死区非线性
死区非线性显示在电机等各种电气设备中,直流伺服电机、执行机构等。死区非线性当输入交叉一定限制值时,请参阅输出变为零的条件。
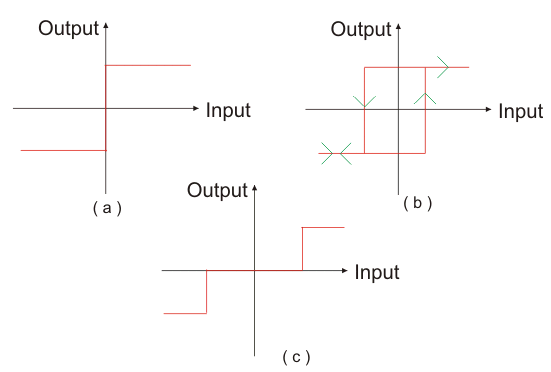
继电器非线性(开/关控制器)
机电继电器经常用于控制系统,其中控制策略需要仅具有两种或三个状态的控制信号。这也称为开/关控制器或两个状态控制器。
继电器非线性(a)开/关(b)开/关带迟滞(c)开/关带死区。图(a)显示了双向继电器的理想特性。在实践中,继电器不会立即响应。对于两个开关瞬间之间的输入电流,继电器可能位于一个位置或另一个位置,这取决于输入的先前历史。这个特性称为开/关和滞后,显示在无花果(b)。继电器也有一定数量的死区在实践中显示在无花果(c),死区是由继电器的磁场绕组需要一个有限的电流将电枢。
强烈的非线性
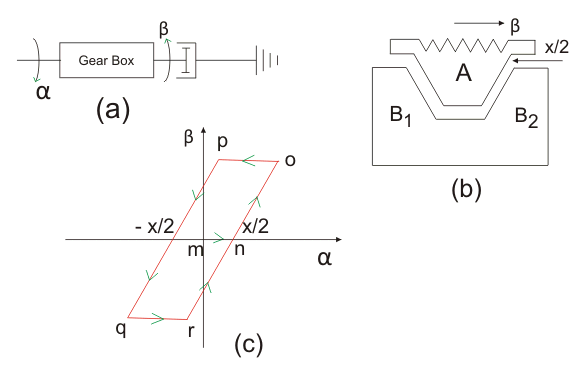
在物理系统中常见的另一个重要非线性是机械传动的滞后,例如齿轮列车和螺纹。这种非线性与磁滞后有些不同,并且通常被称为齿隙非线性.实际上,反弹是驱动齿轮的齿与从动齿轮之间的播放。考虑一个变速箱,如下面的图(a)所示,其具有反向插入(b)所示。
图(b)示出了从牙齿B之间的中间位于牙齿的齿A的齿A1B2从动齿轮的。图(c)给出了输入和输出运动之间的关系。当从这个位置顺时针驱动齿A时,直到齿A与齿B接触,才会产生输出运动1在距离距离X / 2之后的驱动档位。该输出运动对应于图(C)的段MN。在接触之后,如果齿轮比被假定为单位,则从动齿轮通过与驱动齿轮相同的角度逆时针旋转。这由线段否说明。随着输入运动颠倒,牙齿A和B之间的接触1丢失,驱动齿轮立即变得静止,基于负载控制的摩擦力摩擦速度可忽略不计的惯性。
因此,输出运动导致齿A在段OP(C)中所示的反向行进距离X距离x。在牙齿A建立与牙齿B接触之后2,从动齿轮现在更在顺时针方向显示部分pq。当输入运动被逆转时,方向齿轮再次为qr段静止,然后沿着rn跟随驱动齿轮。
描述非线性系统的函数分析
的描述控制系统中的功能方法是由Nikolay Mitrofanovich Kryloy和Nikolay Bogoliubov在1930年发明的,后来由Ralph Kochenburger开发。
的描述函数法在多年来发展起来的求解非线性控制系统的所有解析方法中,这种方法被普遍认为是最实用的方法。该方法基本上是包括奈奎斯特稳定性判据在内的频率响应方法对非线性系统的近似推广。
的描述函数法非线性系统被定义为基础之间的幅度和相位角的复杂比谐波分量输出到输入的正弦信号。我们也可以称之为正弦描述函数。数学上,
在那里,
N =描述函数,
x =输入正弦曲线的幅度,
Y =输出的基本谐波分量的幅度,
φ.1=输出基谐波分量的相移。
让我们讨论描述非线性控制系统功能的基本概念。
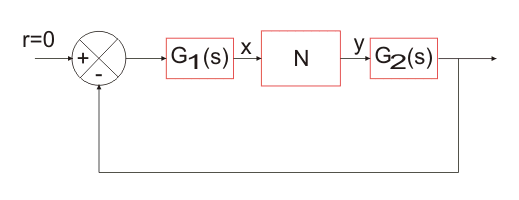
让我们考虑下面这个非线性系统的框图,其中G1(s)和G2(s)表示线性元素,N表示非线性元素。
假设输入x的非线性元素是正弦的,即,
对于这个输入,非线性元素的输出y将是一个非正弦周期函数,可以表示为傅里叶系列作为
大多数非线性是奇对称或奇半波对称的;平均值Y0对于所有这种情况都是零,因此输出将是,
作为G.1G (s)2(s) has low pass characteristics, it can be assumed to a good degree of approximation that all higher harmonics of y are filtered out in the process, and the input x to the nonlinear element N is mainly contributed by fundamental component of y i.e. first harmonics. So in the describing function analysis, we assume that only the fundamental harmonic component of the output. Since the higher harmonics in the output of a non linear system are often of smaller amplitude than the amplitude of fundamental harmonic component. Most control systems are low pass filters, with the result that the higher harmonics are very much attenuated compared with the fundamental harmonic component.
因此,y1只需要考虑。
可以写成y1(t)以
通过使用相量,
系数A.1和B.1的傅里叶系列由,
从描述函数的定义,我们有,
让我们找出这些非线性的描述函数。
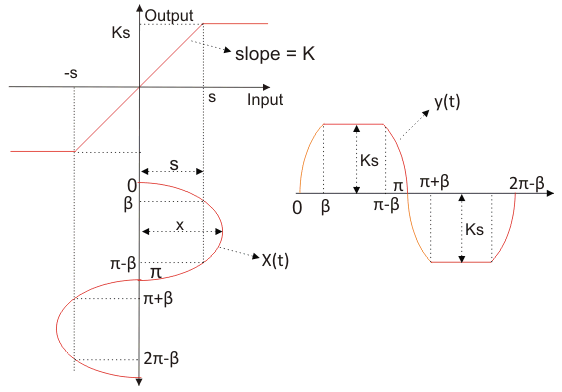
饱和非线性描述函数
如图所示,我们有饱和特性曲线。
我们取输入函数为
现在来自曲线,我们可以将输出定义为:
让我们先计算一下傅里叶系列常数A.1.
代入上述方程的输出值,对函数从0到2π积分,我们得到常数A1的值为零。
类似地,我们可以计算傅里叶常数B的值1对于给定的输出和B的值1可以计算为:
可以计算描述功能的相位角可以计算为
因此,饱和度的描述函数为
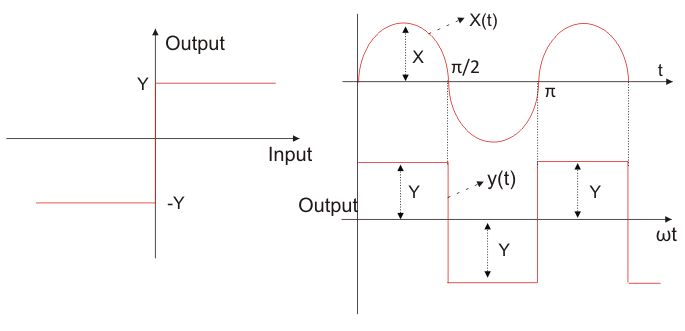
理想继电器的描述功能
我们具有理想继电器的特征曲线,如给定图所示。
我们取输入函数为
现在从曲线我们可以定义输出为
输出周期函数具有奇数对称性:
我们先计算傅里叶级数常数A1.
把输出的值代入上面的方程,对函数从0到2π积分,我们就得到常数A的值1为零。
类似地,我们可以计算傅里叶常数B的值1对于给定的输出和B的值1可以计算为
代替上述等式y(t)= y中的输出的值,我们具有常数b的值1
描述函数的相位角可计算为
因此,理想继电器的描述函数为
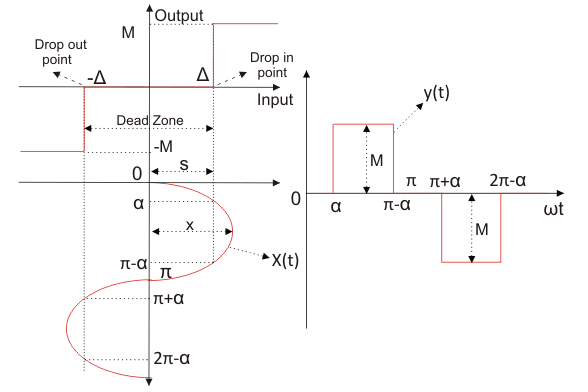
真实继电器(有死区继电器)描述函数
如图所示,我们有真实的特征曲线。如果X小于死区Δ,则继电器不产生输出;的第一个谐波分量傅里叶系列当然是零,描述函数也是零。如果X > Δ继电器产生输出。
我们取输入函数为
现在从曲线我们可以定义输出为
输出周期函数具有奇数对称性:
让我们先计算一下傅里叶系列常数A.1.
把输出的值代入上面的方程,对函数从0到2π积分,我们就得到常数A的值1为零。
类似地,我们可以计算给定输出的傅里叶常数B的值,B的值可以计算为
由于y的对称性,系数B1可以计算如下,
因此,描述函数为
描述反冲非线性的函数
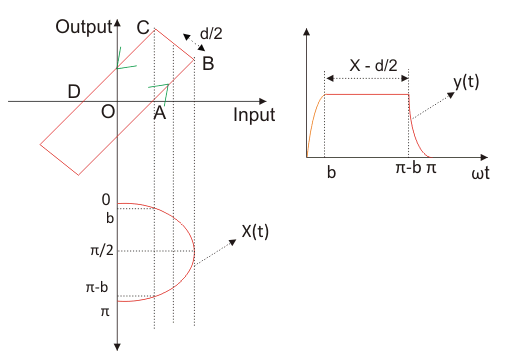
如图所示,我们有齿隙的特性曲线。我们取输入函数为
现在从曲线我们可以定义输出为
让我们先计算一下傅里叶系列常数A.1.
把输出的值代入上面的方程,对函数从0到2π积分,我们就得到常数A的值1作为
类似地,我们可以计算给定输出的傅里叶常数B和B的值1可以计算为
把输出的值代入上面的方程然后对函数从0到积分我们就得到常数B的值1作为
由下式可以很容易地计算出齿隙的描述函数