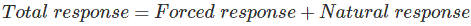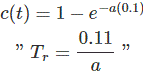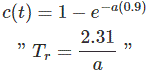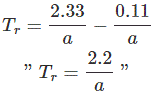目录
优先命令控制系统是什么
A级先令控制系统定义为类型控制系统输入输出关系传输函数)是一个一阶微分方程一阶微分方程包含一阶衍生物,但没有衍生物比一阶高微分方程顺序为方程中最高序衍生物排序
举个例子,让我们看看下文显示的控制系统块图

函数转移(输入输出关系)对控制系统定义如下:
出处 :
- K表示DC增益(输入信号和输出稳定状态值之间的系统比增益)
- T表示时间常量系统时间常量量一阶系统响应单元步进
记住微分方程的顺序是方程中最高顺序衍生物的顺序评估对象.
自此向第一权
上移函数为一阶差分方程上块图表示一阶控制系统
在一个理论替代例子中,让我们表示转移函数等于:
自此例子向二权
函数转移二阶差分方程因此,带上传输函数的控制系统将是一个二阶控制系统.
多数实用模型为一阶系统高阶系统优先第一阶模式可视之为优先阶系统
工程师尝试寻找技术提高系统的效率和可靠性有两种方法控制系统一号开路控制系统中外加闭路反馈控制系统
开放循环系统输入向给定过程并产生输出系统没有回馈 系统“知道”实际输出接近期望输出
在一个闭环控制系统中,系统有能力检查实际输出与期望输出相偏多远稳态报错)传递差数反馈控制器控制系统者控制器将根据反馈调整对系统控制
输入为单元级输出为阶梯响应阶梯响应生成系统瞬态响应清晰视觉有两种系统,一阶系统二阶系统 代表许多物理系统
系统第一阶下定义为时间优先衍生物,时间第二阶下系统第二阶下为时间二次衍生物
一阶系统集成器随着订单数的增加,系统集成器数也增加从数学上讲,它是时间函数的第一个衍生物
使用微分方程或微分方程解析系统方程Laplace变换工程师找到了方法 最小化解方程技术 突发输出和工作效率系统总响应和强制响应和自然响应
强制响应也称稳态响应或特殊方程自然响应也称同质方程
开始讨论前,你应该知道控制工程极概念零概念传输函数和反馈控制系统基本概念提醒内存反馈控制系统基本概念
优先命令控制系统转移函数
A级传输函数表示控制系统输出信号与输入信号之间的关系,表示所有可能的输入值
移位函数波兰
极转移函数Laplace变换值变量导致转移函数无限化
分母函数转换实为函数极
零转移函数
零转移函数为 Laplace变换变量值,导致函数变换为零
位移函数名实为函数零
优先命令控制系统
在此讨论一阶控制系统无零第一阶控制系统告诉我们响应速度 持续时间稳定状态
输入为单元步数Rss=1/s,输出为阶步响应Cs第一级命令控制系统泛方程

有两极,一是输入极ss=0,二是系统线ss=-a,此极为极负轴图MATLABSOFTWARE使用命令pzma
取反向变换令全响应
由输入极源产生强制响应自定义向系统提供强制响应,由系统生成某种响应即强制响应,系统极-a产生自然响应因系统瞬时响应
计算后,这里通用形式一阶系统ss=1-e上传等同强制响应即1和自然响应即e上传.唯一需要查找的是参数a
多技术像微分方程或逆序Laplace变换都解决总响应问题 但这些都耗时费力
极值零值使用和基础概念给我们定性信息解决问题,并由于这些概念,我们可以很容易分辨响应速度和系统时间以达到稳态点
描述三大瞬态响应性能规范 时间常数 上升时间 并安顿时间
时间常量优先控制系统
上头时间常量可定义为步进响应需要时间升至63%或0.63最终值我们称它为t=1/a取时常数对等单位为1/秒或频率
我们称参数a指数频率e-at衍生物-aat=0时间常量被视为瞬态响应规范一阶控制系统.
通过设置极控制响应速度极距虚轴越远 瞬态响应越快因此,我们可以离虚轴远点设置极加速整个过程
起序控制系统
上升时间定义波形从0.1向0.9或10%向90%最终值移动时间方程上升时间,我们分别将0.1和0.9放入通用一阶系统方程
t=0.1
t=0.9
取0.9和0.1之差
方程上升时间if we knew参数a, we can easy file查找系统上升时间
位定优先控制系统
沉积时间定义为响应时间达到并保持在其最终值2%以内百分比限制到最终值的5%两种百分数都考虑
方程安顿时间由T提供s级=4/
通过使用这三个瞬态响应规范, 我们很容易计算系统阶梯响应 正因如此本质技术对顺序系统方程有用
完成优先指令控制系统
学习所有事后一阶控制系统,我们得出以下结论:
- 极输入函数生成强制响应形式正因极源产生级函数输出
- 极传递函数产生自然响应系统极
- 实轴极生成表e-at指数频离原点越远 指数瞬态响应越快 衰减到零
- 使用极和零,我们可以加速系统性能并获取期望输出