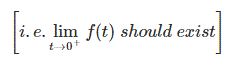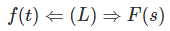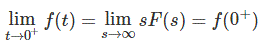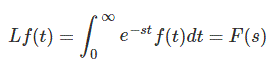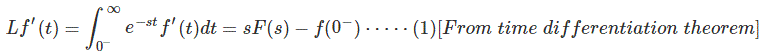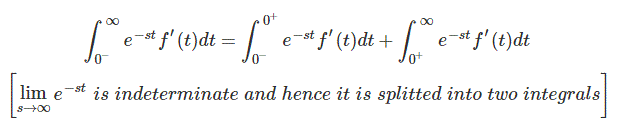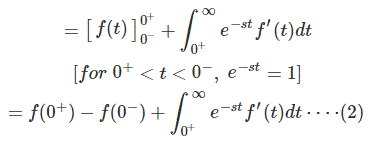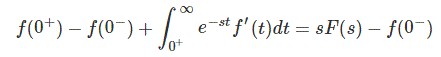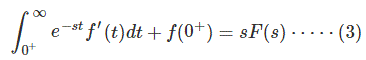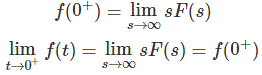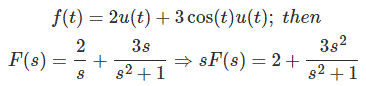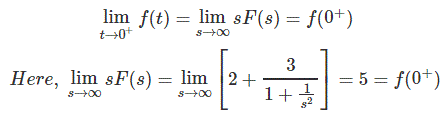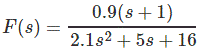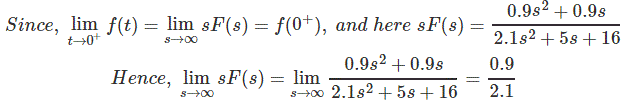初值定理是基本性质之一拉普拉斯变换．它是由著名的法国数学物理学家皮埃尔·西蒙·德·拉普拉斯侯爵提出的。他运用牛顿的万有引力理论，在行星运动领域做出了重要贡献。他的工作关于概率论和统计被认为是开创性的，这影响了整个新一代数学家。有72个人的名字被镌刻在埃菲尔铁塔上，拉普拉斯就是其中之一。
初值定理和终值定理统称为极限定理。初值定理通常被称为IVT。它能让我们找到t =(0)时的初始值+)对于一个给定的变换函数(拉普拉斯)而不让我们更努力地去求f(t)在这种情况下，这是一个繁琐的过程。
初值定理存在的条件
-
- 函数f(t)及其导数f(t)应该是拉普拉斯变换的。
- 如果时间t趋于(0+)则函数f(t)存在。
- 函数f(t) = 0对于t > 0在原点不包含脉冲或高阶奇点。
拉普拉斯初值定理的表述
如果f(t)和f(s)是拉普拉斯变换对。即
的初值定理
拉普拉斯初值定理的证明
函数f(t)的拉普拉斯变换是
那么它的导数f ' (t)的拉普拉斯变换是
首先考虑积分部分
把(2)代入(1)得到
消去f (0- - - - - -)两边都有
我们可以直接写出上面的方程但是我的目的是求∫(0- - - - - -对∞)是，无论我们如何考虑负数的极限，它属于有正值的结果。
注意:
我们也知道拉普拉斯变换只适用于因果函数。
考虑(s)在(3)中两边都趋于无穷
由此证明了初值定理。
初值定理的应用
我之前说过初值定理的目的是确定函数f (t)的初值前提是它的拉普拉斯变换已知
示例1:
求函数f (t) = 2u (t) + 3 cost u (t)的初始值
索尔:
根据初值定理
初始值由5给出。
示例2:
求变换函数的初值
索尔:
根据初值定理
[当s→∞时，s的值变得越来越不显著，因此只需取领先系数的比值即可得到结果]
示例3:
求的初值
解决方案:
初值定理在这种情况下不适用。我们可以用两种方法证明它。
让我们看看结果如何
方法1:
注意:
如果F (s)是真分数，即分子多项式比分母多项式低阶，则此定理是严格适用的。
如果应用IVT，我们得到∞作为初始值。
[这在实际电路中是不可能的]
alit:
应用拉普拉斯逆变换
很明显，初值定理是不适用的，因为存在脉冲函数，它随时间t是常数。
通过本文的讨论，我们可以很容易地利用拉普拉斯变换函数来控制电路的初始条件。
