照明定律（解释和公式）

逆平面照度法

该法律指出，照度（e）在垂直于连接点和源的线的平面上的任何点处与源和平面之间的距离的平方成反比。

其中，我是给定方向的发光强度。

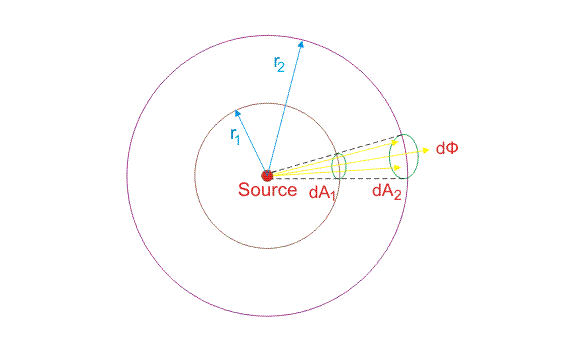
假设光源在任何方向上都有光强为I的光。从这个源取两个距离作为使这个源为中心的半径。

根据上图，两个半径是r₁和R.₂．在距离r₁达₁是拍摄的基本表面积。在这个方向₁，da₂被认为是在r₂距离。
达₁和da₂在具有相同分布式光通量φ的同一实心角Ω内。
面积Da.₁在R.₁接收与区域DA相同的光通量₂在R.₂由于固体是相同的。

再次为两个基本表面的立体角度

距离的照度

距离的照度

现在，从等式（i）我们得到，

现在在等式（III）中，



这表明了点源的已知逆平方法关系。
可以看出，照度与来自源的照明点的正方形相同。
如果光源不是点源，那么我们可以认为这个大来源是许多点源的求和。
这种关系可以应用于所有光源。

余弦照度法则

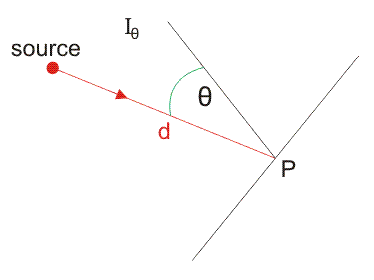
法律指出，平面上的点处的照度与光入射角的余弦成比例（入射光方向与平面正常的角度之间的角度）。

它是点源照度方程。
在哪里，我_θ.是照明点的方向的源的发光强度，ɵ是普通到包含照明点的平面之间的角度以及将源连接到照明点的线，而d是与照明点的距离。

但对于非点来源，可以在光通量而不是发光强度的术语中分析余弦的照度法。
由基本区域接收的光通量的照度或表面密度随着距光源的距离和基本区域相对于光通量方向的距离而变化。
当区域的元素接收到其表面的光通量接收光通量时，会发生最大照度。
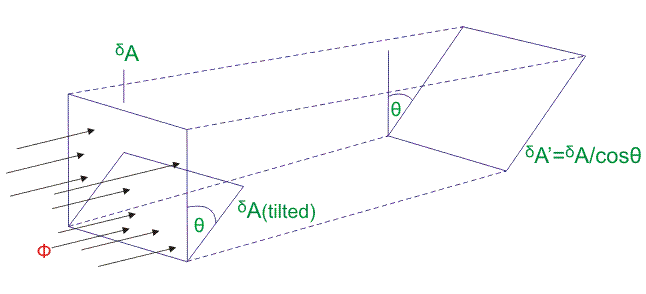
当区域的元素相对于光通量的方向倾斜时，基本表面上的照度或磁通密度减小。这可以用两种方式被认为。

1. 倾斜的基本区域（ΔA）不能拦截先前接收的所有光通量，因此照度下降。
2. 如果基本区域（ΔA）增加，则照度下降。

出于案例（1）当元素Δa被角度倾斜时ɵ的量助势截取的Δa是由

因此，ΔA接收的通量减少了因子Cosɵ。
现在ΔA的照度是

出于案例（2），如果较大元素ΔA截取的所有通量：

所以照明寿命成为

这两种方法都会导致