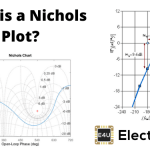
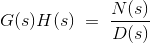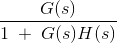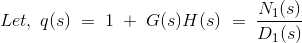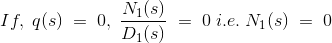什么是奈奎斯特图
一个奈奎斯特图(或奈奎斯特图)是频率响应图,用于控制工程和信号处理。奈奎斯特图通常用于评估具有反馈的系统的稳定性。在笛卡尔坐标系中,实部传递函数在X轴上画,虚部在Y轴上画。频率作为一个参数进行扫频,得到一个基于频率的图。同样的Nyquist图可以用极坐标来描述,其中传递函数的增益为径向坐标,传递函数的相位为相应的角坐标。
反馈的稳定性分析控制系统是基于识别特征方程的根在s平面上的位置。如果根在s平面的左侧,则系统是稳定的。系统的相对稳定性可以通过使用频率响应方法来确定-例如奈奎斯特图和波德图.
的奈奎斯特稳定性判据用来确定特征方程在s平面指定区域内根的存在性。要了解一个奈奎斯特图我们首先需要学习一些术语。注意,复杂平面中的闭合路径称为等高线。
尼奎斯特路径或尼奎斯特轮廓
的奈奎斯特曲线是s平面上的一个封闭轮廓,它完全包围了s平面的整个右半边。为了将s平面的完整RHS包起来,绘制了一条沿jω轴、中心为原点的大半圆路径。半圆的半径被视为奈奎斯特环行。
尼奎斯特包围
如果在等高线内找到一个点,就称它被一条等高线包围着。
尼奎斯特映射
将s平面上的点变换为F(s)平面上的点的过程称为映射,将F(s)变换为映射函数。
如何绘制奈奎斯特图
奈奎斯特图可以通过以下步骤绘制:
- 步骤1 -检查jω轴的G(s) H(s)极点,包括原点的极点。
- 步骤2 -选择合适的奈奎斯特轮廓- a)画一个半径为R的半圆,R趋于无穷,包含s平面的整个右半圆。
- 步骤3 -参考参考确定等高线上的各个分段尼奎斯特路
- 步骤4 -通过在映射函数中代入对应线段的方程来分段执行映射。基本上,我们要画出各自线段的极坐标图。
- 步骤5 -线段的映射通常是+ve虚轴各自路径映射的镜像。
- 步骤6 -覆盖s平面右半圆路径一般映射到G(s) H(s)平面上的一个点。
- 步骤7 -互连所有的映射不同的段,以产生所需的奈奎斯特图.
- 步骤8 -注意(- 1,0)处顺时针环圈的数量,用N = Z - P来确定稳定性
为开环传递函数(O.L.T.F)
为闭环传递函数(C.L.T.F)
N(s) = 0是开环零,D(s)是开环极点
从稳定性的角度来看,闭环极点不应位于s平面的RH侧。特征方程1 + G(s) H(s) = 0表示闭环极点。
现在1 + G(s) H(s) = 0所以q(s)也应该是0。
因此,从稳定性的角度来看,q(s)的零不应该在s平面的RHP中。
为了定义稳定性,考虑了整个RHP(右平面)。考虑到半圆的半径R趋于无穷,我们假设半圆包含了RHP中的所有点。[R→∞)。
理解的第一步应用奈奎斯特准则关于控制系统稳定性的确定,从s平面映射到G(s) H(s) -平面。s被认为是一个独立的复变量,G(s) H(s)的对应值是绘制在另一个复平面G(s) H(s) -平面上的因变量。
因此对于s平面上的每一个点,在G(s) H(s) -平面上都存在一个对应点。在映射过程中,自变量s沿s平面上的指定路径变化,G(s)H(s)平面上相应的点进行连接。这就完成了从s平面映射到G(s)H(s) -平面的过程。
奈奎斯特稳定性判据表示N = Z - p,其中N为总no。对于原点,P是总数。和Z是总数。0。
案例1:N = 0(没有包围),所以Z = P = 0和Z = P
如果N = 0, P必须为0,因此系统是稳定的。
案例2:N > 0(顺时针环行),P = 0, Z≠0,z> P
对于这两种情况,系统都是不稳定的。
案例3:N < 0(逆时针环行),所以Z = 0, P≠0,P = >z
系统是稳定的。