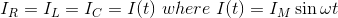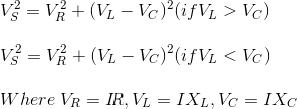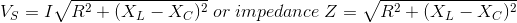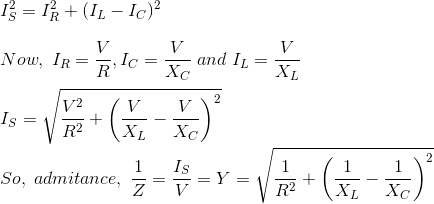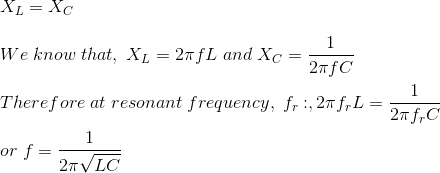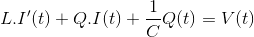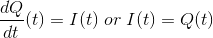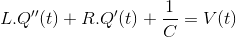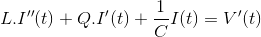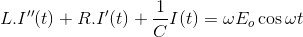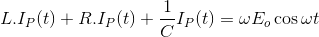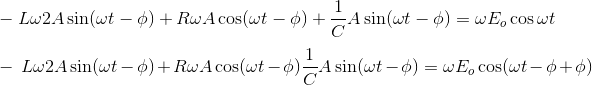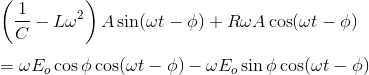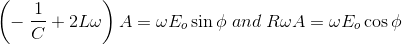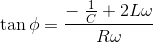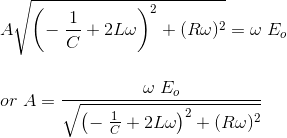在一个RLC电路最基本的元素电阻器,电感器,电容器连接在一个电压供应。所有这些元素都是线性的和被动的。无源元件是那些消耗能量而不是生产;线性元素是那些有一个线性电压和之间的关系当前的。
有多种方式连接这些元素在电压供应,但最常见的方法是连接这些元素串联或并联。的RLC电路展览的性质共振在LC电路展品一样,但是在这个电路振荡模的影响比LC电路由于电路中电阻的存在。
系列RLC电路
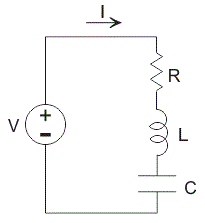
当一个电阻器、电感器和电容器串联连接的电压供给,电路,因此形成系列RLC电路。
因为所有这些组件连接在系列,目前在每个元素是相同的,
让VR是电压电阻器,R。
Vl是电压电感器,L。
VC是电压电容器C。
Xl是归纳电抗。
XC容抗。
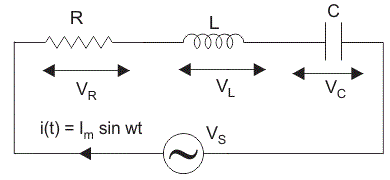
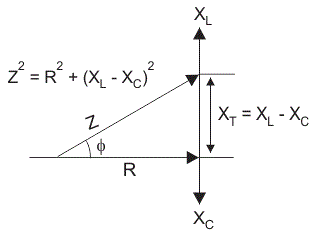
RLC电路的总电压不等于电压的代数和电阻,电感、电容器;但它是一个矢量和,因为在电阻器的电压与电流同相,感应电压使电流的90o电容器,电压滞后电流增加到90人o(根据伊莱冰的人)。
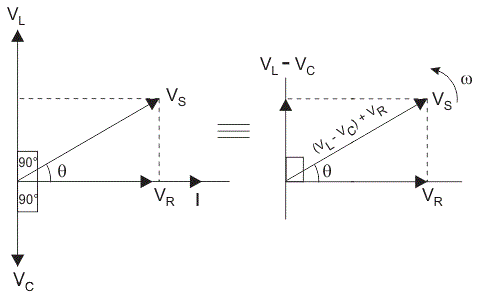
因此,电压在每个组件彼此不相;所以他们不能用算术方法补充道。下图显示了串联RLC电路的相量图。用于绘制RLC串联电路的相量图,目前作为参考,因为每个元素串联电路中通过的电流是相同的和相应的电压向量为每个组件在参考当前常见的向量。
一系列RLC电路的阻抗
一系列RLC电路的阻抗Z定义为反对当前的流动是由于电路电阻R,感抗,Xl和容抗,XC。如果感抗大于电容电抗。e Xl> XC,那么RLC电路相角滞后,如果容抗大于感抗。e XC> Xl然后,RLC电路主要相角,我如果电感和电容都是相同的。e Xl= XC电路就会表现为纯电阻电路。
我们知道
在那里,
替换的值
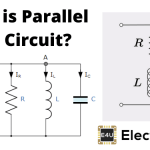
并联RLC电路
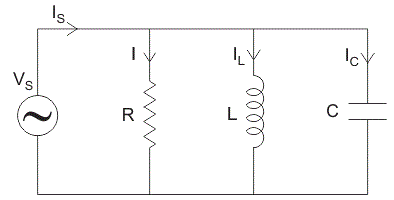
在并联RLC电路是电阻、电感和电容并联在电压供应。并联RLC电路串联RLC电路是完全相反的。外加电压是相同的所有组件和电源电流会分裂。
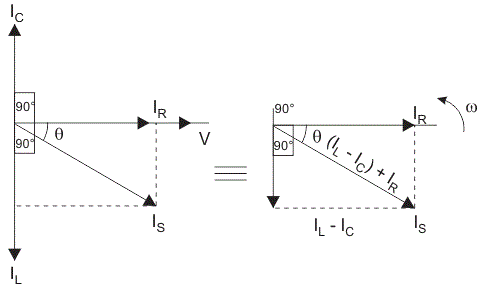
总电流的供应不等于数学和电流的各个组件,但是它等于矢量和电流,电流在电阻、电感和电容不是彼此在同一阶段;所以他们不能用算术方法补充道。
并联RLC电路的相量图,我R电流在电阻R安培。
我C电容器的电流,C安培。
我l电感中的电流,L安培。
我年代是安培的电源电流。
在并联RLC电路中,所有组件连接在平行;所以每个元素的电压是一样的。因此,对于画矢量图,以电压为参考向量和所有其他的电流。e我R,我C,我l是相对于这个电压向量。当前通过每个元素可以使用基尔霍夫电流定律,即电流进入一个结或节点的总和等于离开该节点电流之和。
如上所示的方程阻抗Z并联RLC电路;每个元素都有相互的阻抗(1 / Z)。导纳,y并联RLC电路,方便使用代替阻抗导纳。
共振在RLC电路
在包含电感和电容的电路,能量存储在两种不同的方式。
- 当一个电感电流,能量存储在磁场。
- 当电容器充电,能量存储在静态电场。
电感的磁场是由当前,被提供的放电电容器。同样,电容器充电的电流产生的感应磁场的崩溃,这一过程持续进行,导致电能振荡磁场和电场之间的关系。在某些情况下,在某些特定频率称为共振频率,电路的感抗就等于容抗导致电能振荡电场之间的电容和电感的磁场。这形成了一个谐波振荡器为电流。在RLC电路,电阻的存在导致这些振荡年代消失一段时间,它被称为阻尼电阻的影响。
谐振频率公式
在共振时,在特定的频率称为共振频率,fr。
当发生共振时,电路的感抗就等于容抗,导致电路阻抗最小的系列RLC电路;但当电阻器、电感器和电容器并联连接在一起,电路阻抗变得最大,所以并联RLC电路有时被称为anti-resonator。注意,共振频率最低的一个对象被称为它的振动基频
串联RLC电路和并联RLC电路的区别
| S.NO | RLC串联电路 | RLC并联电路 |
| 1 | 电阻、电感和电容串联连接 | 电阻器、电感器和电容器并联连接 |
| 2 | 目前在每个元素是一样的 | 电流是不同的在所有元素和总电流等于当前我每个分支的矢量和。e我年代2=我R2+(我C——我l)2 |
| 3 | 电压是不同的所有元素和总电压等于电压的矢量和每个组件。e V年代2= VR2+ (Vl- - - - - - VC)2 | 电压每个元素是相同的 |
| 4 | 画矢量图、电流矢量作为参考 | 用于绘制矢量图、电压作为参考向量 |
| 5 | 电压是由每个元素:VRV =红外,lX =我l,VCX =我C | 目前在每个元素是: 我R= V / R,我C= V / XC,我l= V / Xl |
| 6 | 它更方便使用阻抗计算 | 它更方便使用导纳计算 |
| 7 | 在共振,当Xl= XC,电路最小阻抗 | 在共振,当Xl= XC,电路最大阻抗 |
RLC电路方程
考虑一个RLC电路电阻R、电感L、电容C系列,是由一个连接电压源诉让问电容器上的电荷和电流的电路即适用基尔霍夫电压定律
在这个方程;阻力,电感,电容和电压已知数量未知但电流和电荷量。我们知道电流是电荷的流动,所以它是由
区分我' (t) = Q " (t)
区分上述方程' t '我们得到,
现在在时间t = 0时,V(0) = 0和在时间t = t V (t) = Eosinωt
区分对' t '我们得到V (t) =ωEocosωt
替代上面的价值V (t)的方程
让我们说这个方程的解是我P(t) = Asin(ωt -ǿ)如果我P(t)是一个解以上方程,然后它必须满足这个方程
现在用我的价值P(t)和微分得到
因为应用公式(A + B)和结合类似的条款我们得到,
匹配系数罪(ωt -φ),因为(ωt -φ)两岸,
现在我们有两个方程两个未知数。eφ和,将上述两个方程得到,
平方并添加以上方程,我们得到
分析RLC电路使用拉普拉斯变换
步骤1:画一个给定电路的相量图。
步骤2:在RLC串联电路使用基尔霍夫电压定律和现行法律在RLC并联电路的时域微分方程形式。
步骤3:使用拉普拉斯变换这些微分方程从时域转换成s域。
步骤4:寻找未知变量,解决这些方程。
步骤5:应用拉普拉斯逆变换将从s域方程转化为时域。
RLC电路的应用
它被用作低通滤波器,高通滤波器,带通滤波器带阻滤波器,电压乘法器和振荡器电路。用于调优广播或音频接收器。