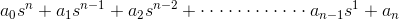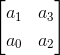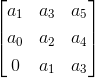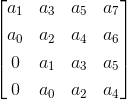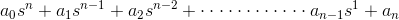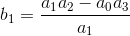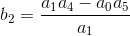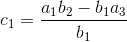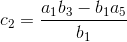阅读理论后网络综合,我们可以很容易地说,系统的任意极点位于s平面原点的右侧,这使得系统不稳定。在这个条件的基础上,a . Hurwitz和E.J.Routh开始研究系统稳定的充要条件。我们将讨论系统稳定性的两个判据。第一个标准是A. Hurwitz给出的,这个标准也被称为Hurwitz稳定性准则或Routh Hurwitz (R-H)稳定性准则.
赫维茨判据
在特征方程的帮助下,我们将制作一些赫尔维茨决定因素,以便找出系统的稳定性。我们将系统的特性方程定义为
现在有n个行列式TH.订单特征方程。
让我们看看我们如何从特征方程的系数中写出决定簇。k的步骤步骤TH.阶特征方程为:
决定因素:该决定因素的价值由| A1|哪里A.1s的系数是多少N-1在特征方程。
决定因素二:这个行列式的值是
这里每行中的元素数等于确定性号码,我们在这里具有决定因素是两个。第一行由前两个奇数系数和第二行组成,第二行由前两个偶数系数组成。
决定因素三:这个行列式的值是
这里每一行的元素数等于行列式数这里的行列式数是3。第一行由前三个奇系数组成,第二行由前三个偶系数组成,第三行由第一个元素为零,其余两个元素为前两个奇系数组成。
决定因素四:这个行列式的值是,
这里每行中的元素数等于确定性号码,我们在这里具有决定因素是四个。第一行由前三个四个系数组成,第二行由前四个偶数系数组成,第三行由第一元素组成为零,其剩余的三个元素作为前三个奇数系数,第四行由第一元素组成零和三个元素作为前三个偶数系数。
按照相同的程序,我们可以概括决定因素。决定簇的一般形式如下:
现在为了检查上述系统的稳定性,计算每个决定簇的值。如果每个决定因素的值大于零,则系统将是稳定的,即,即每个决定因素的值应该是正的。在所有其他情况下,系统都不会稳定。
Routh稳定标准
该标准也称为修改了系统稳定性的修改了urwitz标准。我们将在两部分中研究这一标准。第一部分将涵盖系统稳定性的必要条件,第二部分将涵盖系统稳定性的充分条件。让我们再次考虑系统的特征方程
1)第一部分(系统稳定性的必要条件):在此,我们有两个条件,如下所示:
- 特征方程的所有系数都必须是正的实数。
- 特征方程的所有系数都不为零。
2)第两部分(系统稳定性的充分条件):让我们首先构造routh数组。为了构造routh数组,遵循以下步骤:
- 第一行将包括特征方程的所有偶数条款。将它们从第一(甚至是术语)排列到最后(甚至是术语)。第一行写下面:a0.一种2一种4.一种6.............
- 第二行将包括特征方程的所有奇数项。将它们从第一(奇数)排列到持续的(奇数项)。第一行写下面:a1一种3.一种5.一种7............
- 第三行的元素可以计算为:
(1)第一要素:用一个0.利用下一列的对角线相反的元件(即a3.)然后从A的产品中减去它1和一个2(其中A.2是对角线上的下一列元素)然后最后用a这样除结果得到吗1.数学上,我们写成第一个元素
(2)第二个元素:用一个0.与下一列旁边的对角线相反的元件(即a5.)然后从A的产品中减去它1和一个4.(在那里,4.对角线上挨着下一列元素)然后最后用a这样除结果得到吗1.数学上我们写成第二元素
同样,我们可以计算第三行的所有元素。
(d)第四行元素可按下列程序计算:
(1)第一要素:用b1利用下一列的对角线相反的元件(即a3.)然后从A的产品中减去它1和b2(在那里,b2是对角线上的下一列元素)然后最后用b除以结果这样得到吗1.数学上,我们写成第一个元素
(2)第二个元素:用b1与下一列旁边的对角线相反的元件(即a5.)然后从A的产品中减去它1和b3.(在那里,b3.对角线上挨着下一列元素)然后最后用a这样除结果得到吗1.数学上我们写成第二元素
同样,我们可以计算第四行的所有元素。
同样,我们可以计算所有行的所有元素。
稳定标准如果第一列的所有元素为正为正,则系统将是稳定的。但是,如果他们中的任何人都是负数,系统将是不稳定的。
现在有一些与Routh稳定标准相关的特殊情况,如下所述:
(1)案例一:如果数组中任意一行的第一项为零,而该行的其余部分至少有一个非零项。
在这种情况下,我们将假设一个非常小的值(ε),其趋于零代替零。通过用(ε)替换零,我们将计算Routh数组的所有元素。在计算所有元素之后,我们将在包含(ε)的每个元素处应用限制。在解决每个元素的限制如果我们将获得积极限制值,那么我们将说给定的系统在所有其他条件下都稳定,我们会说给定的系统不稳定。
(2)病例二:当Routh数组中任意一行的所有元素都为零时。在这种情况下,我们可以说系统具有边际稳定的症状。让我们首先理解任意一行的所有元素都为零的物理意义。物理意义是在s平面上有对称分布的特征方程根。现在为了找出这种情况下的稳定性,我们首先要找出辅助方程。辅助方程可以通过使用Routh数组中零行上方的行元素来形成。求出辅助方程后,对辅助方程求导,得到零行元素。如果用辅助方程所形成的新路径阵中没有符号变化,则认为该系统是有限稳定的。而在其他情况下,我们会说,给定的系统是不稳定的。