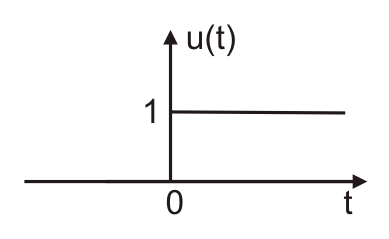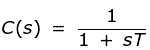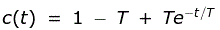当我们研究分析的时候控制系统的瞬态状态和稳态响应知道一些基本术语非常重要,这些是下面描述的。
标准输入信号:这些也称为测试输入信号。输入信号本质上是非常复杂的,这是复杂的,因为它可以是各种其他信号的组合。因此,通过应用这些信号非常难以分析任何系统的特征性能。因此,我们使用测试信号或标准输入信号非常容易处理。与非标准输入信号相比,我们可以轻松分析任何系统的特征性能。现在有各种类型的标准输入信号,它们是如下所写的:
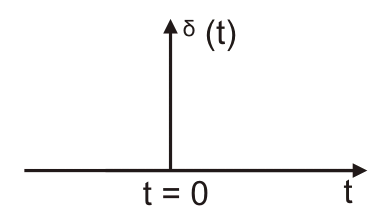
单元脉冲信号:在时域中,它由∂(t)表示。这拉普拉斯变换单位脉冲函数是1,并且与单元脉冲功能相关联的相应波形如下所示。
单位步骤信号:在时域中,它由U(T)表示。单位阶跃函数的拉普拉斯变换是1 / s,与单位步进功能相关的相应波形如下所示。
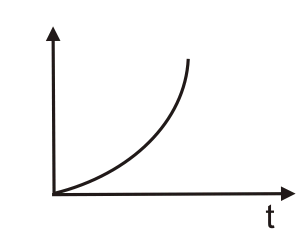
单位斜坡信号:在时域中,它由R(t)表示。单位斜坡函数的拉普拉斯变换是1 / s2与单元斜坡功能相关联的相应波形如下所示。
抛物线类型信号:在时域中,它由t表示2/ 2。抛物线类型的Laplace变换函数是1 / s3.与抛物线类型相关联的相应波形如下所示。
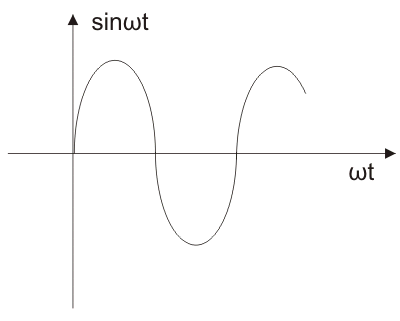
正弦型信号:在时域中,它由SIN(ωt)表示。LAPPALL的正弦类型的功能是ω/(s2+ω.2)和与函数的正弦类型相关联的相应波形如下所示。
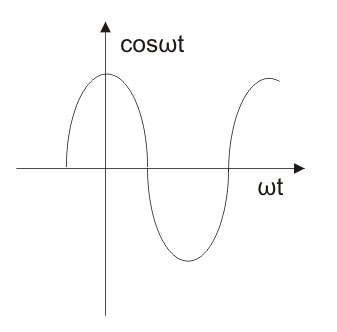
余弦类型的信号:在时域中,它由COS(ωt)表示。LAPPAlt变换的余弦类型的功能是ω/(s2+ω.2)和与功能的余弦类型相关联的相应波形如下所示,
现在处于描述两种类型的响应,这是一个时间的响应。
控制系统的瞬态响应
顾名思义控制系统的瞬态响应意味着改变所以,这主要发生在两个条件之后,并且这两个条件写得如下 -
- 条件一:在将输入信号应用于系统的输入信号时,刚切换“ON”。
- 条件第二:在任何异常情况下。异常情况可能包括负载,短路等突然变化。
控制系统的稳态响应
系统结算后发生稳定状态,在稳定系统开始正常工作后。控制系统的稳态响应是输入信号的函数,它也被称为强制响应。
现在瞬态响应控制系统清楚地描述了系统功能期间的功能控制系统的瞬态状态和稳态响应可以清楚地描述系统在稳态期间如何运行的描述。因此,两个国家的时间分析非常重要。我们将分别分析答复类型。让我们首先分析瞬态响应。为了分析瞬态响应,我们有一些时间规范,它们写得如下:
延迟时间 :这次是由t表示的D.。响应所需的时间是第一次达到最终值的50%,这次被称为延迟时间。在时间响应规范曲线中清楚地显示延迟时间。
上升时间:这次是由t表示的R.,并且可以使用的计算上升时间公式。我们在两种情况下定义上升时间:
- 在沉积系统下的情况下,在ζ的值小于一个的情况下,在这种情况下,上升时间被定义为响应从零值达到百分之百的最终值所需的时间。
- 在d d的衰减系统的情况下,在这种情况下,在这种情况下,上升时间被定义为响应达到达到百分之九十百分之九十百分之九十的值所需的时间。
高峰时段:这次是由t表示的P.。响应首次达到峰值所需的时间,这次被称为峰值时间。在时间响应规范曲线中清楚地示出了峰值时间。
安定时间:这次是由t表示的S.,并且可以使用的计算建立时间公式。第一次,响应响应和在指定范围内的响应在其最终价值的规定范围内,这次被称为稳定时间。在时间响应规范曲线中清楚地示出了稳定时间。
最大过冲:它以稳态值的百分比表示(一般),并且它被定义为响应的最大正偏差。这里所需的值是稳态值。
稳态错误:随着时间倾向于Infinity的实际输出和所需输出之间的差异定义为infinity.now我们正当到我们执行一排序系统的时间响应分析。
一阶控制系统的瞬态状态和稳态响应
让我们考虑第一订单系统的框图。
从这个框图中,我们可以找到整体转换功能这是线性本质上的。第一订单系统的传递函数是1 /((ST + 1))。我们将分析控制系统对以下标准信号的稳态和瞬态响应。
- 单位脉冲。
- 单位步骤。
- 单位斜坡。
单位脉冲响应:我们有单位冲动的拉普拉斯变换是1.现在让我们将这个标准输入给第一订单系统,我们有
现在采用上述等式的逆拉普拉斯变换,我们有
很清楚控制系统的稳态响应仅取决于时间常数't',它是自然腐烂的。
单位步骤响应:我们的LAPPAlt变换为单位脉冲是1 / s。现在让我们将这个标准输入给第一订单系统,我们有
在部分分数的帮助下,采取上述等式的逆拉普拉斯变换,我们有
很明显,时间响应仅取决于时间常数't'。在这种情况下,通过将极限T趋于零,稳态误差为零。
单位斜坡响应:我们有单位冲动的拉普拉斯变换是1 / s2。现在让我们将这个标准输入给第一订单系统,我们有
在部分分数的帮助下,采取我们的上述等式的逆拉普拉斯变换
通过将极限T绘制的时间绘制时间的指数函数,趋于零。
二阶控制系统的瞬态状态和稳态响应
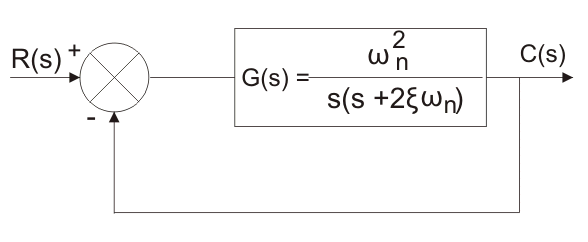
让我们考虑二阶系统的框图。
从这个框图中,我们可以找到整体传递函数,它是非线性的。二阶系统的传递函数是(ω2/ {s(s +2νω)}。我们将分析控制系统的瞬态状态响应对于以下标准信号。
单位脉冲响应:我们有一个单位冲动的拉普拉斯变换是1.现在让我们把这个标准输入给二阶系统,我们有
其中,ω是rad / sec的自然频率,并且ζ是阻尼比。
单位步骤响应:我们的LAPPAlt变换为单位脉冲是1 / s。现在让我们将这个标准输入给第一订单系统,我们有
现在我们将看到ζ响应的不同价值的影响。我们基于不同价值的ζ的三种系统。
- 在阻尼系统下:当ζ的值小于一个时,据说系统被置于阻尼系统下。在这种情况下,根部是复杂的,实际部分总是负。系统是渐近稳定的。上升时间比其他系统较小,存在有限的过冲。
- 严重阻尼系统:当ζ的值是一个时,据说系统被批判性地阻尼系统。在这种情况下,根部是真实的,并且实际部分总是在自然中重复。系统是渐近稳定的。在该系统中,上升时间较少,没有有限的过冲。
- 过度阻尼系统:当ζ的值大于1时,据说系统被置于阻尼系统上。在这种情况下,根部是真实的,在自然中拼凑而实际,实际部分总是消极的。系统是渐近稳定的。上升时间大于其他系统,没有有限的过冲。
- 持续振荡:当Zeta的值为零时,据说系统据说是维持阻尼系统。在这种情况下,不会发生阻尼。
现在让我们通过针对二阶系统的单位步骤输入导出上升时间,峰值时间,最大过冲,建立时间和稳态误差的表达式。
上升时间 :为了导出上升时间的表达式,我们必须等同于C(T)= 1.从上面的表达式
在解决上面的方程上,我们对上升时间的表达等于
高峰时段 :在区分C(t)的表达上,我们可以获得峰值时间的表达。DC(t)/ dt = 0我们有峰值时间的表达,
最大过冲:现在,从图中可以清楚地看出,在峰值时间TP时会出现最大过冲,因此在放置峰值时间的值时,我们将获得最大的过冲
安定时间:建立时间由表达给出
稳态错误:稳态误差是在实际输出和所需输出之间的衍射,因此在趋于无穷大时,稳态误差为零。