内容
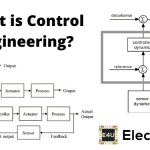
什么是控制器?
控制器是一种机制,它寻求最小化系统的实际值(即过程变量)和系统的期望值(即设定值)之间的差异。控制器是最基本的部分控制工程并在所有的络合物中使用控制系统.
在我们详细介绍各种控制器之前,了解控制器在控制系统理论中的应用是非常必要的。控制器的重要用途包括:
- 控制器通过减小稳态误差来提高稳态精度。
- 随着稳态精度的提高,稳定性也随之提高。
- 控制器还有助于减少系统产生的不需要的偏移。
- 控制器可以控制系统的最大超调量。
- 控制器可以帮助减少系统产生的噪声信号。
- 控制器可以帮助加快过阻尼系统的缓慢响应。
这些控制器的不同变种被编成了法典工业汽车等设备可编程序逻辑控制器和SCADA系统.下面将详细讨论各种类型的控制器。
类型的控制器
有两种主要类型的控制器:连续控制器和不连续控制器。
在不连续控制器中,操纵变量在离散值之间变化。根据被操纵变量可以假定的不同状态的数量,可以区分两位置、三位置和多位置控制器。与连续控制器相比,断续控制器操作非常简单,可切换最终控制元件。
连续控制器的主要特点是被控变量(也称为操纵变量)可以在控制器的输出范围内具有任何值。在连续函数中控制器的理论,整个控制动作发生的基本模式有三种:
- 比例控制器.
- 积分控制器.
- 微分控制器.
我们使用这些模式的组合来控制我们的系统,使过程变量等于设定值(或尽可能接近我们能得到的值)。这三种类型的控制器可以组合成新的控制器:
- 比例积分控制器(PI控制器)
- 比例和微分控制器(PD控制器)
- 比例积分导数控制(PID控制器)
现在我们将在下面详细讨论每一种控制模式。
比例控制器
所有控制器都有一个最适合它们的特定用例。我们不能仅仅在任何系统中插入任何类型的控制器就期望一个好的结果——必须满足某些条件。对于一个比例控制器,有两种情况,分别写在下面:
- 偏差不宜过大;也就是说,输入和输出之间不应该有很大的偏差。
- 偏离不应是突然的。
现在我们有条件来讨论比例控制器,正如它的名字所暗示的,比例控制器的输出(也称为驱动信号)是直接正比于误差信号。现在让我们从数学上分析比例控制器。我们知道在比例控制器中输出与误差信号成正比,用数学方法写出来,

去掉这个比例符号,

Kp是比例常数,也称为控制器增益。
建议Kp应该保持大于团结。如果是k的值p大于单位(>1),则将误差信号放大,从而便于检测放大后的误差信号。
比例控制器的优点
现在让我们来讨论一下比例控制器的一些优点。
- 比例控制器有助于减小稳态误差,从而使系统更加稳定。
- 在这些控制器的帮助下,过阻尼系统的慢响应可以变得更快。
比例控制器的缺点
现在这些控制器有一些严重的缺点,写如下:
- 由于这些控制器的存在,我们在系统中得到一些偏移。
- 比例控制器也增加了系统的最大超调。
现在,我们将用一个独特的例子来解释比例控制器(p -控制器)。通过这个例子,读者对“稳定性”和“稳态误差也会增强。考虑如图-1所示的反馈控制系统

“K”称为比例控制器(也称为误差放大器)。该控制系统特性方程为:
年代3.+ 3年代2+ 2 s + K = 0
如果在这个特征方程中应用Routh-Hurwitz,那么稳定性的“K”范围为0
根轨迹上述控制系统如图-2所示

(你可以理解根轨迹为开环传递函数(G(s)H(s)绘制,但给出了闭环传递函数的极点的概念,即特征方程的根,也称为特征方程的零。根轨迹有助于设计' K '的值,即比例控制器的增益)。因此,对于K= 0.2、1、5.8等值,系统(图-1)是稳定的;但是我们应该选择什么值。我们将分析每个值并向您显示结果。作为一个总结,您可以理解,“K”的高值(例如,K=5.8)会降低稳定性(这是一个缺点),但会提高稳态性能(即减少稳态误差,这是一个优点)。
你们可以理解
,稳态误差(e党卫军)=
(适用于步进输入的情况)
,稳态误差(e党卫军)=
(在斜坡输入时适用)
,稳态误差(e党卫军)=
(适用于抛物型输入)
可以看出,当K值较大时,Kp、Kv、Ka值较大,稳态误差较小。
现在我们将对每个案例进行分析并解释其结果
1.在K = 0.2
在这种情况下,系统的特征方程为s3.+ 3年代2+ 2 s + 0.2 = 0;这个方程的根是-2。088 -0。7909 -0。1211;我们可以忽略-2.088(因为它远离虚轴)。在剩下的两个根的基础上,它可以被称为一个过阻尼系统(因为两个根都是实数和负数,没有虚部)。针对阶跃输入,其时间响应如图3所示。可以看出,响应没有振荡。(如果根是复数,则时间响应呈现振荡)。过阻尼系统的阻尼大于“1”。

在本例中,开环传递函数为
它的增益裕度(GM)=29.5 dB,相裕度(PM)=81.5°,
需要注意的是,在设计控制系统时,不宜选用过阻尼系统。根(闭环传递函数的极点)应该有轻微的虚部。在过阻尼的情况下,阻尼大于‘1’,阻尼在0.8左右为佳。
2.在K = 1
在这种情况下,系统的特征方程为s3.+ 3年代2+ 2 + 1 = 0;这个方程的根是-2.3247,-0.3376±j0.5623;我们可以忽略-2。3247。在剩下的两个根的基础上,它可以被称为欠阻尼系统(因为两个根都是具有负实部的复数)。针对阶跃输入,其时间响应如图-4所示。

在本例中,开环传递函数为
其增益边际(GM)=15.6 dB,阶段保证金(PM) = 53.4°,
3.在K = 5.8
因为5.8非常接近6,所以你可以理解系统是稳定的,但几乎是在边界上。你可以找到它的特征方程的根。一个根可以忽略,剩下的两个根将非常接近虚轴。(其特征方程的根为-2.9816,-0.0092±j1.39)。对于阶跃输入,它时间响应如图5所示。

在本例中,开环传递函数为
它的增益裕度=0.294 db, Phase Margin =0.919°
可以分析,与之前的案例相比,GM & PM大幅减少。由于系统非常接近不稳定,因此GM & PM也非常接近于零值。
积分控制器
顾名思义积分控制器输出(也称为致动信号)与误差信号的积分成正比。现在让我们在数学上分析整体控制器。正如我们在整体控制器输出中所知,与错误信号的集成成正比,在数学上写出我们有,

去掉这个比例符号,

其中ki是一个作为控制器增益的积分常数。积分控制器也称为复位控制器。
积分控制器的优点
由于其独特的能力,积分控制器可以返回控制变量回到一个干扰后的确切设定点,这就是为什么这些被称为复位控制器。
积分控制器的缺点
它倾向于使系统不稳定,因为它对产生的错误反应缓慢。
衍生控制器
我们从来没有使用微分控制器一个人。它应该与其他控制器模式组合使用,因为它的缺点如下:
- 它永远不会改善稳态误差。
- 它产生饱和效应,也放大了系统中产生的噪声信号。
现在,正如名字所暗示的,在一个微分控制器的输出(也称为驱动信号)是直接正比于误差信号的导数。现在让我们从数学上分析微分控制器。我们知道微分控制器的输出与误差信号的导数成正比,用数学方法写出来,

去掉这个比例符号,

在那里,Kd是比例常数,也称为控制器增益。微分控制器也称为速率控制器。
导数控制器的优点
衍生控制器的主要优点是它可以提高系统的瞬态响应。
比例积分控制器
顾名思义,它是一个比例和积分控制器的组合,输出(也称为执行信号)等于比例和积分的误差信号之和。现在让我们从数学上分析比例和积分控制器。我们知道在一个比例积分控制器中输出正比于误差的比例和误差信号的积分的总和,用数学方法写出来,

去掉这个比例符号,

在那里,K我和K.p分别是比例常数和积分常数。
优点和缺点是比例和积分控制器的优点和缺点的组合。
通过PI控制器,我们在原点添加一个极点,在远离原点的某个地方(在复平面的左手边)添加一个零。由于极点在原点,其效果会更大,因此PI控制器可能会降低稳定性;但它的主要优点是大大减少了稳态误差,因此是应用最广泛的控制器之一。
PI控制器原理图如图-6所示。对于阶跃输入,当K=5.8时,K我=0.2,其时间响应如图-7所示。在K=5.8时(作为一个P控制器,它处于不稳定的边缘,所以仅仅通过添加一个积分部分的小值,它就变得不稳定。请注意,Integral部分降低了稳定性,这并不意味着系统将永远不稳定。在本例中,我们增加了一个组成部分,系统变得不稳定)。


比例和微分控制器
顾名思义,它是一个比例和微分控制器的组合,输出(也称为驱动信号)等于比例和误差信号的导数之和。现在让我们从数学上分析比例和微分控制器。我们知道在一个比例和微分的控制器中输出直接正比于误差的比例和误差信号的微分的总和,从数学上写出来,

去掉这个比例符号,

在那里,Kd和Kp比例常数和导数常数。
优点和缺点是比例和导数控制器的优点和缺点的组合。
读者应该注意,在开环传递函数中适当的位置增加“零”可以提高稳定性,而在开环传递函数中增加极点可能会降低稳定性。上面这句话中的“在适当的位置”是非常重要的,这叫做控制系统的设计(即在复杂平面的适当点上加上零点和极点,以得到理想的结果)。
插入PD控制器就像在开环传递函数[G(s)H(s)]中添加零。PD控制器示意图如图-8所示

在本例中,我们取K=5.8, Td=0.5的值。针对阶跃输入,其时间响应如图-9所示。可以比较图-9和图-5,了解在P-controller中插入导数部分的效果。

PD控制器的传递函数为K+Tds或Td(s+K/Td);所以在-K/Td时我们加了一个0。通过控制“K”或“Td”的值,可以确定“零”的位置。如果‘零’非常远离虚轴,其影响将减少,如果“零”是虚轴(或非常接近虚轴)它也将不接受(根轨迹一般都从“两极”开始与终止“零”,设计师的目的通常是这样,根轨迹不应该用于虚轴,由于这个原因,“零”非常接近虚轴也是不可接受的,因此“零”的适当位置应该保持)
一般来说,PD控制器改善了控制系统的暂态性能,PI控制器改善了控制系统的稳态性能。
比例积分导数控制器(PID控制器)
PID控制器通常用于工业控制应用,以调节温度、流量、压力、速度和其他过程变量。

PID控制器的传递函数为:
或者
可以观察到原点的一个极点是固定的,剩下的参数TdK和Ki决定了两个0的位置。在这种情况下,我们可以按照要求保留两个复零或两个实零,因此PID控制器可以提供更好的整定。在过去,PI控制器是控制工程师的最佳选择之一,因为PID控制器的设计(参数整定)有点困难,但如今,由于软件的发展,PID控制器的设计已经成为一个简单的任务。
对于阶跃输入,当K=5.8时,K我= 0.2, Td=0.5,其时间响应如图-11所示。比较图-11和图-9(我们取了一些值以便比较所有的时间响应)。

PID控制器设计的一般准则
在为给定系统设计PID控制器时,获得期望响应的一般指导原则如下:
- 得到闭环传递函数的瞬态响应,确定需要改进的地方。
- 插入比例控制器,通过Routh-Hurwitz或合适的软件设计“K”值。
- 添加一个整体部件以减少稳态误差。
- 增加导数部分以增加阻尼(阻尼应该在0.6-0.9之间)。导数部分将减少超调和瞬态时间。
- MATLAB中可用的Sisotool也可用于适当的调优,并获得所需的总体响应。
- 请注意,上述参数调整步骤(设计控制系统)是一般准则。设计控制器没有固定的步骤。
模糊逻辑控制器
模糊逻辑控制器(FLC)使用在系统是高度非线性。一般来说,大多数物理系统/电气系统都是高度非线性的。由于这个原因,模糊逻辑控制器是一个很好的选择。
FLC不需要精确的数学模型。它的工作输入基于过去的经验,可以处理非线性,可以提出的干扰不灵敏度比大多数其他非线性控制器。
FLC基于模糊集,即对象的类别,其中从隶属关系到非隶属关系的过渡是平滑的,而不是突然的。
在最近的发展中,FLC已经在复杂、非线性或未定义系统中优于其他具有良好实践知识的控制器。因此,模糊集的边界可能是模糊的和有歧义的,使它们对近似模型有用。模糊控制器综合过程中的重要步骤是根据以往的经验或实际知识定义输入和输出变量。
这是相应地完成的,使用控制器的预期功能。没有一般规则来选择这些变量,尽管通常所选择的变量是受控系统的状态,它们的错误,误差变化和错误累积。