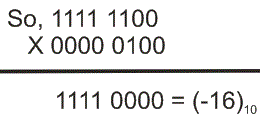2的补充有一个有趣的财产二进制算术可以在符号或无符号的数字上轻松进行操作。它产生了正确的2种补充结果。
如何在2的补充中代表十进制数?
让我们拿一个号码。负符号表示数字是该数字的数量为零。采用我们最熟悉的数字系统的例子是十进制系统。
在哪里,
在二进制系统中,只有两位数0和1二元系统每个数字及其标志都是仅使用这两位0和1.由于否定标志不能直接写入二进制系统,因此我们必须找到一些代表它们的替代方法。
为此,我们利用了负数的定义。如果我们必须代表否定二进制数,我们必须找到一个二进制数量,其中原始无符号或正二进制数为零。随着这两个数字的总和为零,第二个数字被视为第一数量的负等同物。
假设我们必须在二进制中写入 - 5为5或+ 5。现在5或+ 5可以用二进制字节或8位系统表示为0000 0101和零在二进制字节或8位系统中表示为0000 0000。
因此,该结果是( - 5)的表示10.。
现在让我们检查2的补充0000 0101,这是
因此,证明了零减去任何二进制数量只不过是2个数字的补充,因此2的补充二进制数可以表示为该数字的负等同物。在2的补充中,首先我们将十进制数转换为二进制数系。假设我们想代表(5)10.进入二元2的补充。二进制表示(5)10.是(0000 0101)2。
现在有趣的事实是未签名的形式(5)10.进入2的补充是(5)的二元形式的直接代表10.即(0000 0101)2。未签名的数字被视为正数。签名十进制数可以是正数或负数。现在计算2的补充对于签名的十进制数,即(-5)10.,我们必须找出1的补充然后将每个数字转换为其相对的数字(即1进入0或0到1),并最后添加1。此结果添加后是2的签名(负)十进制数的完整表示。
现在看下面的图表。
(+5)10.与(5)相同10.。但对于(-1)10.它被视为无符号(255)10.。(-5)10.⇔(251)10.
始终将其保持在心灵中,负2的补充号码始终以这样的方式表示为二进制数,即当添加到相同的幅度的正数时必须为零。
重要的是要保持在头脑中,最左键或有效位表示整数的符号。它也称为符号位。
- 如果左列最大位为零,则该数字为正。
- 如果左列最低位为一个,则数字为负。
2的补体方法中的算术
2的补充补充
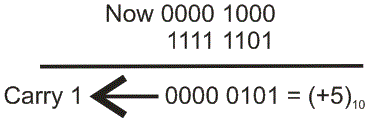
在2的补充中添加,它总是遵循与正常使用的相同规则二进制添加。假设我们要添加(8)10.(-3)10.。
首先,我们必须将它们转换为2的补充并只需添加它们。
携带是1,那么数字是正的。这里携带是1,它超出了8位,因此不考虑在字节中,因此答案是一个字节长的正数。因此,很明显,对于签名和未签名的数字,可以在2的补充中轻松进行添加。
2的补充减法
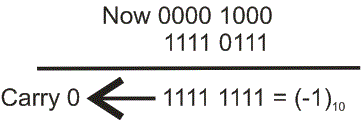
在2的补充中减法遵循相同的规则,因为它处于正常二进制添加。唯一的是,这里的subtrahend首先将其转换为否定形式,然后将其添加到minuend。假设我们要减去(8)10.来自(9)10.。首先转换(8)10.来自(-9)10.进入2的补充,简单地添加。
携带是0然后数字是负的。所以很明显,可以容易地进行减法2的补充容易地。
2的补充倍增
对于2的补充乘法,它始终遵循与相同的规则二进制乘法。假设我们想要乘以( - 4)10.与(4)10.给出(-16)10.。现在,( - 4)10.= 1111 1100在2的补充中和(4)10.= 0000 0100在2的补充中
2的补充部门
对于2的补充划分,该方法反复是2的补充减法。首先计算第2分部的补充,然后将增加该转换的除款。现在来到下一个减法周期。这里商品取代股息。再次重复它,再次达到商量太小或零。如果它不是零,那么它被视为余数。假设我们想计算(7)10.÷(3)10.,回答给出(2)10.作为商和(1)10.余数。现在让我们开始计算它2的补充。
随着重复的是两轮,那么商就是(2)10.。